题目内容
若函数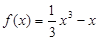 在
在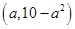 上有最小值,则实数
上有最小值,则实数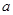 的取值范围是 .
的取值范围是 .
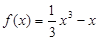 在
在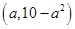 上有最小值,则实数
上有最小值,则实数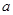 的取值范围是 .
的取值范围是 . 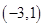
解:由题意可得:函数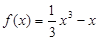 ,
,
所以f′(x)=x2-1.
因为函数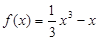 在区间
在区间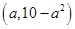 上有最小值,
上有最小值,
所以函数f(x)在区间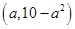 内先减再增,即f′(x)先小于0然后再大于0,
内先减再增,即f′(x)先小于0然后再大于0,
所以结合二次函数的性质可得:a<1<10-a2,
解得:-3<a<1.
故答案为(-3,1).
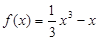 ,
,所以f′(x)=x2-1.
因为函数
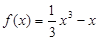 在区间
在区间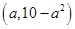 上有最小值,
上有最小值,所以函数f(x)在区间
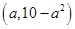 内先减再增,即f′(x)先小于0然后再大于0,
内先减再增,即f′(x)先小于0然后再大于0,所以结合二次函数的性质可得:a<1<10-a2,
解得:-3<a<1.
故答案为(-3,1).

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
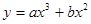 ,当
,当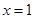 时,有极大值
时,有极大值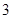 ;
;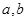 的值;(2)求函数
的值;(2)求函数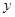 的极小值。
的极小值。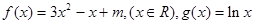
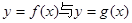 有公共切线时,求函数
有公共切线时,求函数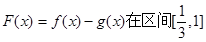 上的最值
上的最值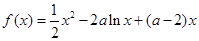 ,
,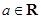 .
.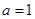 时,求函数
时,求函数 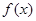 的最小值;
的最小值; 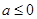 时,讨论函数
时,讨论函数 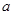 ,对任意的
,对任意的 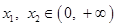 ,且
,且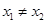 ,有
,有 ,恒成立,若存在求出
,恒成立,若存在求出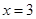 是函数
是函数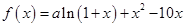 的一个极值点.
的一个极值点.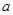 ;
;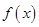 的单调区间;
的单调区间;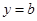 与函数
与函数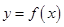 的图象有3个交点,求
的图象有3个交点,求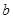 的取值范围.
的取值范围.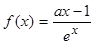 .
.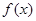 的单调区间;
的单调区间;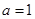 时,若方程
时,若方程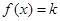 有两个不同的实根
有两个不同的实根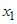 和
和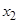 ,
,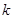 的取值范围;
的取值范围;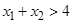 .
.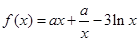 .
.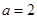 时,求函数
时,求函数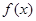 的最小值;
的最小值;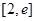 上单调递增,求实数
上单调递增,求实数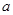 的取值范围.
的取值范围.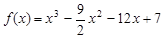 的单调递增区间.
的单调递增区间.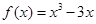 ,(1)求函数
,(1)求函数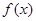 极值.(2)求函数
极值.(2)求函数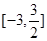 上的最大值和最小值.
上的最大值和最小值.