题目内容
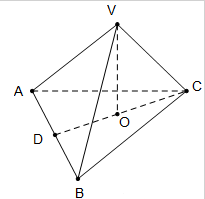 如图,三棱锥V-ABC中,VO⊥平面ABC,O∈CD,AB=4,AD=BD,VA=VB=
如图,三棱锥V-ABC中,VO⊥平面ABC,O∈CD,AB=4,AD=BD,VA=VB=| 13 |
| 29 |
(1)求证:CD⊥AB;
(2)求证:VC⊥平面ABV.
考点:直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由VO⊥平面ABC,得到VO⊥AB,连接VD,只要证明AB⊥平面VCD即可;
(2)由(1)可得VC⊥AB,再由计算证明VC⊥VD,利用线面垂直的判定定理证明.
(2)由(1)可得VC⊥AB,再由计算证明VC⊥VD,利用线面垂直的判定定理证明.
解答:
证明:(1)∵VO⊥平面ABC,∴VO⊥AB,连接VD,∵AD=BD,VA=VB,∴AB⊥VD,∴AB⊥平面VCD,∴AB⊥CD;
(2)∵AB=4,AD=BD=2,VA=VB=
,BC=
,VC=4.AB⊥CD,∴CD=
=5,VD=
=3,
∴VD2+VC2=CD2,∴VC⊥VD,
由(1)知VC⊥AB,由AB∩VD=D,
∴VC⊥平面ABV.
(2)∵AB=4,AD=BD=2,VA=VB=
| 13 |
| 29 |
| BC2-BD2 |
| VA2-AD2 |
∴VD2+VC2=CD2,∴VC⊥VD,
由(1)知VC⊥AB,由AB∩VD=D,
∴VC⊥平面ABV.
点评:本题考查了三棱锥中线线垂直和线面垂直的判定定理的运用,体现了转化的思想.

练习册系列答案
相关题目
若集合A={x||x|≤1},B={x|
≤0},则A∩B为( )
| x-2 |
| x |
| A、[-1,0) |
| B、(0,1] |
| C、[0,2] |
| D、[0,1] |
下列函数中,在区间(0,+∞)上为增函数的是( )
| A、y=ln(x+3) | ||
B、y=-
| ||
C、y=(
| ||
D、y=
|