题目内容
已知双曲线C:
-
=1过点(2,3),且一条渐近线的倾斜角为
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)设双曲线C的左顶点为A1,右焦点为F2,P为双曲线C右支上一点,求
•
的最小值.
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
(Ⅰ)求双曲线C的方程;
(Ⅱ)设双曲线C的左顶点为A1,右焦点为F2,P为双曲线C右支上一点,求
| PA1 |
| PF2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)把点的坐标代入双曲线方程,由渐近线的倾斜角为
得到a,b的关系,联立方程组求得a,b的值,则
双曲线C的方程;
(Ⅱ)由双曲线的方程求得左顶点和右焦点的坐标,设出P的坐标,求出对应向量的坐标,代入数量积整理,配方后由P得横坐标的范围得答案.
| π |
| 3 |
双曲线C的方程;
(Ⅱ)由双曲线的方程求得左顶点和右焦点的坐标,设出P的坐标,求出对应向量的坐标,代入数量积整理,配方后由P得横坐标的范围得答案.
解答:
解:(Ⅰ)∵双曲线C:
-
=1过点(2,3),
∴
-
=1 ①,
又一条渐近线的倾斜角为
,即
=tan
=
②,
联立①②得:a2=1,b2=3.
∴双曲线C的方程为x2-
=1;
(Ⅱ)由(Ⅰ)知:A1(-1,0),F2(2,0),
设P(x0,y0),
则
=(-1-x0,-y0),
=(2-x0,-y0),
∴
•
=(-1-x0)(2-x0)+y02
=x02-x0+y02-2=4x02-x0-5=4(x0-
)2-
,
∵x0≥1,
∴当x0=1时,
•
有最小值为-2.
| x2 |
| a2 |
| y2 |
| b2 |
∴
| 4 |
| a2 |
| 9 |
| b2 |
又一条渐近线的倾斜角为
| π |
| 3 |
| b |
| a |
| π |
| 3 |
| 3 |
联立①②得:a2=1,b2=3.
∴双曲线C的方程为x2-
| y2 |
| 3 |
(Ⅱ)由(Ⅰ)知:A1(-1,0),F2(2,0),
设P(x0,y0),
则
| PA1 |
| PF2 |
∴
| PA1 |
| PF2 |
=x02-x0+y02-2=4x02-x0-5=4(x0-
| 1 |
| 8 |
| 81 |
| 16 |
∵x0≥1,
∴当x0=1时,
| PA1 |
| PF2 |
点评:本题考查了双曲线方程的求法,考查了平面向量的数量积运算,训练了利用配方法求函数的最值,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
,那么f[f(-2)]=( )
|
| A、-16 | B、16 | C、2 | D、-2 |
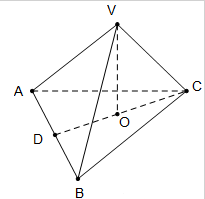 如图,三棱锥V-ABC中,VO⊥平面ABC,O∈CD,AB=4,AD=BD,VA=VB=
如图,三棱锥V-ABC中,VO⊥平面ABC,O∈CD,AB=4,AD=BD,VA=VB= 如图所示,已知抛物线y=x2的动弦AB所在直线与圆x2+y2=1相切,分别过点A、B的抛物线的两条切线相交于点M,求点M的轨迹方程.
如图所示,已知抛物线y=x2的动弦AB所在直线与圆x2+y2=1相切,分别过点A、B的抛物线的两条切线相交于点M,求点M的轨迹方程.