题目内容
已知点P(-2,-3)和以Q为圆心的圆(x-m+1)2+(y-3m)2=4.
(1)求证:圆心Q在过点P的定直线上;
(2)当m为何值时,以PQ为直径的圆过原点?
(1)求证:圆心Q在过点P的定直线上;
(2)当m为何值时,以PQ为直径的圆过原点?
考点:圆方程的综合应用
专题:计算题,证明题,直线与圆
分析:(1)求得圆心Q,令x=m-1,y=3m,消去m,即可得证;
(2)由于以PQ为直径的圆过原点,则OP⊥OQ,运用两直线垂直则斜率之积为-1,解方程,即可得到所求值.
(2)由于以PQ为直径的圆过原点,则OP⊥OQ,运用两直线垂直则斜率之积为-1,解方程,即可得到所求值.
解答:
(1)证明:圆(x-m+1)2+(y-3m)2=4的圆心Q(m-1,3m),半径为2,
令x=m-1,y=3m,消去m,得,y=3(x+1),
代入P点(-2,-3)显然成立,
则圆心Q在过点P的定直线上;
(2)解:由于以PQ为直径的圆过原点,
则OP⊥OQ,
由点P(-2,-3)和Q(m-1,3m),
则有kOP•kOQ=-1,
即有
•
=-1,
解得,m=
.
则有当m为
时,以PQ为直径的圆过原点.
令x=m-1,y=3m,消去m,得,y=3(x+1),
代入P点(-2,-3)显然成立,
则圆心Q在过点P的定直线上;
(2)解:由于以PQ为直径的圆过原点,
则OP⊥OQ,
由点P(-2,-3)和Q(m-1,3m),
则有kOP•kOQ=-1,
即有
| 3 |
| 2 |
| 3m |
| m-1 |
解得,m=
| 2 |
| 11 |
则有当m为
| 2 |
| 11 |
点评:本题考查圆的方程和运用,考查直线和圆的位置关系,两直线垂直的条件,考查运算能力,属于基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
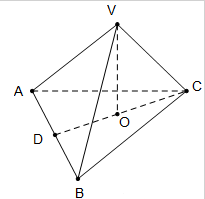 如图,三棱锥V-ABC中,VO⊥平面ABC,O∈CD,AB=4,AD=BD,VA=VB=
如图,三棱锥V-ABC中,VO⊥平面ABC,O∈CD,AB=4,AD=BD,VA=VB=