题目内容

设变量x，y满足约束条件
2x+y-2≥0
x-2y+4≥0
x-1≤0
，则目标函数z=2y-3x的最大值为
4
4
．
分析：画出满足条件的可行域，求出可行域内各角点的坐标，分别代入目标函数，比较后可得目标函数的最大值．
解答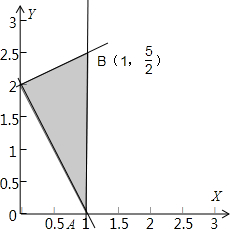：解：满足约束条件
2x+y-2≥0
x-2y+4≥0
x-1≤0
的可行域如图所示：
∵函数z=2y-3x
∴zA=-3，zB=2，zC=4，
即目标函数z=2y-3x的最大值为4
故答案为：4
点评：本题考查的知识点是简单的线性规划，其中角点法是解答此类问题最常用的方法，一定要熟练掌握．
练习册系列答案
相关题目
设变量x，y满足约束条件
y≤2
3
x-3y≤0
x+
3
y-2
3
≥0
，则目标函数u=x2+y2的最大值M与最小值N的比
M
N
=（　　）
A、
4
3
3
B、
16
3
3
C、
4
3
D、
16
3
设变量x，y满足约束条件
x+y≥2
x≤1
y≤2
，则目标函数z=-x+y的最大值是（　　）
（2013•河西区一模）设变量x、y满足约束条件
y≥0
x-y+1≥0
x+y-3≤0
，则z=2x+y的最大值为
6
6
．
（理科）设变量x，y满足约束条件
2x-y≤0
x-3y+5≥0
x≥0
，则目标函数z=x-y的最大值为（　　）
（2012•江西模拟）设变量x，y满足约束条件
x+1≥0
x-y+1≤0
x+y-2≤0
，则z=4x+y的最大值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网