题目内容
在边长为2的正方形ABCD内任取一点P，则点P到正方形中心O的距离小于1的概率为
．
| π |
| 4 |
| π |
| 4 |
分析：先求出正方形的面积，以及满足条件的区域面积，再根据几何概型的概率公式解之即可．
解答：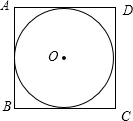
解：正方形的面积为4，即D区域的面积为4；
在正方形内到点O的距离小于1，即为以O点为圆心，1为半径的圆
其面积为π，即d的区域面积为π；
由几何概型的概率公式可知P=
=
故答案为：
．
解：正方形的面积为4，即D区域的面积为4；在正方形内到点O的距离小于1，即为以O点为圆心，1为半径的圆
其面积为π，即d的区域面积为π；
由几何概型的概率公式可知P=
| d |
| D |
| π |
| 4 |
故答案为：
| π |
| 4 |
点评：本题考查几何概型的计算，关键是审清题意，明确符合条件的点的区域．
练习册系列答案
相关题目
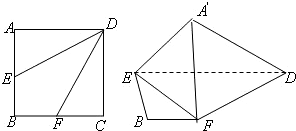
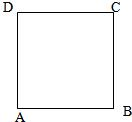在边长为2的正方形ABCD的边上有动点M，从点B开始，沿折线BCDA向A点运动，设M点运动的距离为x，△ABM的面积为S．
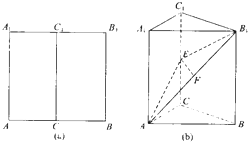如图（a）所示，在边长为2的正方形ABB1A1中，C，C1分别是AB，A1B1的中点，现将正方形ABB1A1沿CC1折叠，使得平面ACC1A1⊥平面CBB1C1，连接AB，A1B1，AB1，如图（b）所示，F是AB1的中点，E是CC1上的点．