题目内容
如图,在边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点,将△AED,△CDF分别沿DE,DF折起,使A,C两点重合于A′.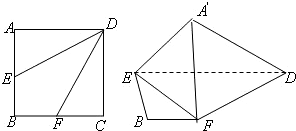
(1)求证:A′D⊥EF;
(2)求二面角A′-EF-D的正切值.
分析:(1)欲证A′D⊥EF,先证A′D⊥面A′EF,根据直线与平面垂直的判定定理可知只需证A′D与面A′EF内两相交直线垂直,而A′D⊥A′E,A′D⊥A′F,满足定理条件;
(2)取EF的中点G,连A′G,DG,根据二面角平面角的定义可知∠A′GD为二面角A′-EF-D的平面角,在Rt△A′GD中求出此角的正切值即可.
(2)取EF的中点G,连A′G,DG,根据二面角平面角的定义可知∠A′GD为二面角A′-EF-D的平面角,在Rt△A′GD中求出此角的正切值即可.
解答: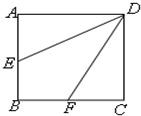 解:(1)证明:∵AD⊥AE,DC⊥CF
解:(1)证明:∵AD⊥AE,DC⊥CF
∴A′D⊥A′E,A′D⊥A′F∴A′D⊥面A′EF,而EF?面A′EF
∴A′D⊥EF
(2)解:取EF的中点G,连A′G,DG,如图
∵AE=CF,
∴A′E=A′F,
∴GA′⊥EF又由(1)知A′D⊥EF,
∴EF⊥面A′GD,EF⊥GD
∴∠A′GD为二面角A′-EF-D的平面角
在△A′EF中,A′E=A′F=1,EF=
∴∠EA′F=90°,
∴A′G=
EF=
又A′D=AD=2在Rt△A′GD中,
tan∠A′GD=
=2
即二面角A′-EF-D的正切值为2
.
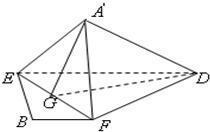
 解:(1)证明:∵AD⊥AE,DC⊥CF
解:(1)证明:∵AD⊥AE,DC⊥CF∴A′D⊥A′E,A′D⊥A′F∴A′D⊥面A′EF,而EF?面A′EF
∴A′D⊥EF
(2)解:取EF的中点G,连A′G,DG,如图
∵AE=CF,
∴A′E=A′F,
∴GA′⊥EF又由(1)知A′D⊥EF,
∴EF⊥面A′GD,EF⊥GD
∴∠A′GD为二面角A′-EF-D的平面角
在△A′EF中,A′E=A′F=1,EF=
| 2 |
∴∠EA′F=90°,
∴A′G=
| 1 |
| 2 |
| ||
| 2 |
tan∠A′GD=
| A′D |
| A′G |
| 2 |
即二面角A′-EF-D的正切值为2
| 2 |

点评:本题主要考查了二面角及其度量,以及空间中直线与直线之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
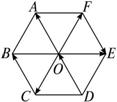
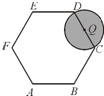 如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量
如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量| AP |
| AB |
| AF |
| A、(1,2] |
| B、[5,6] |
| C、[2,5] |
| D、[3,5] |
 (2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量
(2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量