题目内容
在边长为2的正方形SG1G2G3中,F,E分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合点记为G,则四面体S-EFG的体积是( )
分析:根据题意,在折叠过程中,始终有SG1⊥G1E,SG3⊥G3F,即SG⊥GE,SG⊥GF,由线面垂直的判定定理,易得SG⊥平面EFG,然后求出四棱锥的体积即可得到选项.
解答: 解:∵在折叠过程中,
解:∵在折叠过程中,
始终有SG1⊥G1E,SG3⊥G3F,
即SG⊥GE,SG⊥GF,
所以SG⊥平面EFG.四面体的底面积为:S△EFG=
GE•GF,高为SG=2
∴四面体S-EFG的体积:VS-EFG=
×
× 1×1×2=
.
故选A.
 解:∵在折叠过程中,
解:∵在折叠过程中,始终有SG1⊥G1E,SG3⊥G3F,
即SG⊥GE,SG⊥GF,
所以SG⊥平面EFG.四面体的底面积为:S△EFG=
| 1 |
| 2 |
∴四面体S-EFG的体积:VS-EFG=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
故选A.
点评:线线垂直可由线面垂直的性质推得,直线和平面垂直,得到折叠后三棱锥的高,考查几何体的体积的求法.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 在边长为2的正方形ABCD的边上有动点M,从点B开始,沿折线BCDA向A点运动,设M点运动的距离为x,△ABM的面积为S.
在边长为2的正方形ABCD的边上有动点M,从点B开始,沿折线BCDA向A点运动,设M点运动的距离为x,△ABM的面积为S.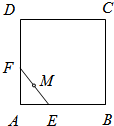 如图,设线段EF的长度为1,端点E、F在边长为2的正方形ABCD的四边上滑动.当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G围成的面积为S,则S=
如图,设线段EF的长度为1,端点E、F在边长为2的正方形ABCD的四边上滑动.当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G围成的面积为S,则S=