题目内容
已知p:存在x∈R,mx2+1≤0;q:对任意x∈R,x2+mx+1>0,若p或q为假,则实数m的取值范围为( )
| A.m≤-2 | B.m≥2 |
| C.m≥2或m≤-2 | D.-2≤m≤2 |
B
解:若p真则m<0;
若q真,即x2+mx+1>0恒成立,
所以△=m2-4<0,
解得-2<m<2.
因为p或q为假命题,所以p,q全假.
所以有m≥0或m≤-2或m≥2
所以m≥2.故选B
若q真,即x2+mx+1>0恒成立,
所以△=m2-4<0,
解得-2<m<2.
因为p或q为假命题,所以p,q全假.
所以有m≥0或m≤-2或m≥2
所以m≥2.故选B

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
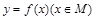 是奇函数”的否定是( )
是奇函数”的否定是( )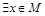 ,
,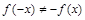
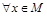 ,
, 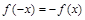
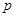 :关于
:关于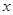 的不等式
的不等式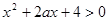 ,对一切
,对一切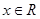 恒成立,命题
恒成立,命题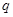 :函数
:函数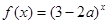 是增函数,若
是增函数,若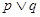 为真,
为真,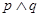 为假,求实数
为假,求实数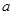 的取值范围.
的取值范围. 的必要非充分条件;
的必要非充分条件; 中,A>B是sinA>sinB的充要条件;
中,A>B是sinA>sinB的充要条件; 的充分非必要条件;
的充分非必要条件; 的充要条件.
的充要条件. ,
, ,且
,且 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围. 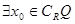 ,
,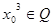 ”的否定是 ( )
”的否定是 ( )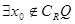 ,
,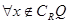 ,
,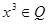
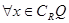 ,
,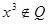
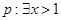 ,
,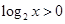 ,则
,则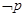 为 .
为 . 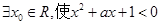 ”的否定是( )
”的否定是( )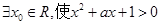
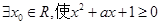
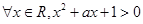 成立
成立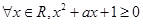 成立
成立