题目内容
已知数列![]() 是首项
是首项![]() 的等比数列,其前
的等比数列,其前![]() 项和
项和![]() 中
中![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,若
,若![]() ≤
≤![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
(1)![]() ;(2)
;(2) ![]() 的最小值为
的最小值为![]() .
.
解析:
(1)若![]() ,则
,则![]() 显然
显然![]() ,
,![]() ,
,![]() 不构成等差数列---1分
不构成等差数列---1分
∴![]() ,当
,当![]() 时,由
时,由![]() ,
,![]() ,
,![]() 成等差数列得
成等差数列得![]()
∴![]()
![]()
![]()
![]() ,∵
,∵![]() ,∴
,∴![]()
∴![]() .
.
(2)∵![]() ,∴
,∴![]()
∴![]() =
=![]()
=![]()
![]()
由![]() ≤
≤![]() 得
得![]() ≤
≤![]() ∴
∴![]() ≥
≥![]()
又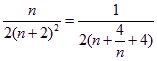 ≤
≤![]()
∴![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
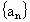 是首项a且公比q不等于1的等比数列,
是首项a且公比q不等于1的等比数列, 是其前n项和,
是其前n项和,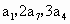 成等差数列.
成等差数列.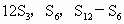 成等比数;
成等比数;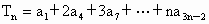 .
. 是首项为1,公差为
是首项为1,公差为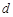 的等差数列,数列
的等差数列,数列 是首项为1,公比为
是首项为1,公比为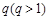 的等比
的等比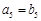 ,
,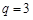 ,求数列
,求数列 的前
的前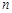 项和;
项和;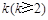 ,使得
,使得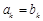 .试比较
.试比较 与
与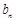 的大小,并说明理由.
的大小,并说明理由. =p(p为正常数,n∈N*),则称{an}为“等方比数列”.若数列{an}是等方比数列则数列{an}必是等比数列.
=p(p为正常数,n∈N*),则称{an}为“等方比数列”.若数列{an}是等方比数列则数列{an}必是等比数列.