题目内容
给出下列一些说法:(1)已知△ABC中,acosB=bcosA,则△ABC为等腰或直角三角形.
(2)已知△ABC中,acosA=bcosB,则△ABC为等腰或直角三角形.
(3)已知数列{an}满足
 =p(p为正常数,n∈N*),则称{an}为“等方比数列”.若数列{an}是等方比数列则数列{an}必是等比数列.
=p(p为正常数,n∈N*),则称{an}为“等方比数列”.若数列{an}是等方比数列则数列{an}必是等比数列.(4)等比数列{an}的前3项的和等于首项的3倍,则该等比数列的公比为-2.
其中正确的说法的序号依次是 .
【答案】分析:(1)直接利用正弦定理,化简表达式,通过两角和与差的三角函数化简,即可判断三角形的形状.
(2)根据正弦定理把等式acosA=bcosB的边换成角的正弦,再利用倍角公式化简整理得sin2A=sin2B,进而推断A=B,或A+B=90°.
(3)若{an} 为“等方比数列”,说明数列{an2}成公比为p的等比数列,而数列{an}的符号不能确定,故不一定成等比数列
(4)利用等比数列的通项公式,建立等式,即可求得等比数列的公比.
解答:解:(1)因为在△ABC中,acosB=bcosA,由正弦定理可知,sinBcosA=sinAcosB,
所以sin(A-B)=0,所以A-B=π,或A=B,因为A,B是三角形内角,所以A=B,三角形是等腰三角形,故(1)错误;
(2)根据正弦定理可知∵acosA=bcosB,
∴sinAcosA=sinBcosB
∴sin2A=sin2B
∴A=B,或2A+2B=180°即A+B=90°,
所以△ABC为等腰或直角三角形,故(2)正确;
(3)若数列{an} 为“等方比数列”,设足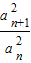 =p=1
=p=1
可得数列{an} 的各项的绝对值相等,但符号不能确定.
比如:1,1,-1,-1,1,1,-1,-1,…,
就是一个等方比数列,而不是等比数列,故(3)错误;
(4)设等比数列的首项为a1,公比为q,则a1+a1q+a1q2=3a1,
∵a1≠0,∴1+q+q2=3,∴q2+q-2=0
∴q=-2或q=1,故(4)错误.
故答案为:(2)
点评:本题主要考查了正弦定理的应用、等比数列的通项与求和等知识,属中档题.
(2)根据正弦定理把等式acosA=bcosB的边换成角的正弦,再利用倍角公式化简整理得sin2A=sin2B,进而推断A=B,或A+B=90°.
(3)若{an} 为“等方比数列”,说明数列{an2}成公比为p的等比数列,而数列{an}的符号不能确定,故不一定成等比数列
(4)利用等比数列的通项公式,建立等式,即可求得等比数列的公比.
解答:解:(1)因为在△ABC中,acosB=bcosA,由正弦定理可知,sinBcosA=sinAcosB,
所以sin(A-B)=0,所以A-B=π,或A=B,因为A,B是三角形内角,所以A=B,三角形是等腰三角形,故(1)错误;
(2)根据正弦定理可知∵acosA=bcosB,
∴sinAcosA=sinBcosB
∴sin2A=sin2B
∴A=B,或2A+2B=180°即A+B=90°,
所以△ABC为等腰或直角三角形,故(2)正确;
(3)若数列{an} 为“等方比数列”,设足
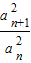 =p=1
=p=1可得数列{an} 的各项的绝对值相等,但符号不能确定.
比如:1,1,-1,-1,1,1,-1,-1,…,
就是一个等方比数列,而不是等比数列,故(3)错误;
(4)设等比数列的首项为a1,公比为q,则a1+a1q+a1q2=3a1,
∵a1≠0,∴1+q+q2=3,∴q2+q-2=0
∴q=-2或q=1,故(4)错误.
故答案为:(2)
点评:本题主要考查了正弦定理的应用、等比数列的通项与求和等知识,属中档题.

练习册系列答案
相关题目