题目内容
20．因式分解：x3+3x-4．分析 原式分组为x3-1+3（x-1），再利用立方差公式、提取公因式即可得出．
解答 解：原式=x3-1+3（x-1）
=（x-1）（x2+x+1）+3（x-1）
=（x-1）（x2+x+4）．
点评 本题考查了利用乘法公式因式分解，考查了计算能力，属于基础题．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
10．已知直线y=kx-2k-1与直线x+2y-4=0的交点位于第一象限，则k的取值范围是（ ）
| A． | -$\frac{3}{2}$＜k＜$\frac{1}{2}$ | B． | k＞$\frac{1}{2}$或k＜-$\frac{3}{2}$ | C． | k≥$\frac{1}{2}$或k≤-$\frac{3}{2}$ | D． | k＞-$\frac{1}{6}$ |
11．
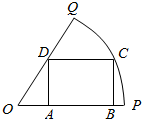如图所示，扇形OPQ的半径为2，圆心角为$\frac{π}{3}$，C是扇形弧上的动点，四边形ABCD是扇形的内接矩形，则SABCD的最大值是（ ）
如图所示，扇形OPQ的半径为2，圆心角为$\frac{π}{3}$，C是扇形弧上的动点，四边形ABCD是扇形的内接矩形，则SABCD的最大值是（ ）| A． | $\frac{2\sqrt{3}}{3}$ | B． | 2$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | $\frac{2}{3}$ |
9．过点A（1，2）且与点P（3，2）距离最大的直线方程是（ ）
| A． | x+2y+1=0 | B． | 2x-y-1=0 | C． | y=1 | D． | x=1 |