��Ŀ����
16����֪��F��1��0������PΪƽ���ϵĶ��㣬����P��ֱ��l��x=-1�Ĵ��ߣ�����ΪH����$\overrightarrow{HP}$•$\overrightarrow{HF}$=$\overrightarrow{FP}$•$\overrightarrow{FH}$����1����P�Ĺ켣C�ķ��̣�
��2�����P�Ĺ켣C��x�ύ�ڵ�M����A��B�ǹ켣C�����ڵ�M�IJ�ͬD�����㣬������$\overrightarrow{MA}$•$\overrightarrow{MB}$=0����A��B���ֱ����켣C�����߽��ڵ�N�����N�Ĺ켣E�ķ��̣�
��3���ڣ�2���������£���֤��kMN•kABΪ��ֵ��
���� ��1����$\overrightarrow{HP}•\overrightarrow{HF}=\overrightarrow{FP}•\overrightarrow{FH}$��չ����������ʽ�ɵ�$|\overrightarrow{HP}|=|\overrightarrow{FP}|$����֪��PΪ�߶�HF�д����ϵĵ㣬�������߶���ɵö���P�Ĺ켣CΪ��FΪ����������ߣ�
�䷽��Ϊy2=4x��
��2����ֱ��MA��б��Ϊk��k��0����д��ֱ��MA�ķ��̣����������������$A��\frac{4}{k^2}��\frac{4}{k}��$����һ���������NA�ķ��̣�ͬ���������NB�ķ��̣�����������ý���N�Ĺ켣���̣�
��3���ɣ�2�����N�����꣬������������б�ʹ�ʽ���kMN��kAB�ô𰸣�
��� ��1���⣺��$\overrightarrow{HP}•\overrightarrow{HF}=\overrightarrow{FP}•\overrightarrow{FH}$�ɵã�$|\overrightarrow{HP}|•|\overrightarrow{HF}|cosPHF=|\overrightarrow{FP}|•|\overrightarrow{FH}|cosPFH$��
��$|\overrightarrow{HP}|=|\overrightarrow{FP}|$����֪��PΪ�߶�HF�д����ϵĵ㣬�ʶ���P�Ĺ켣CΪ��FΪ����������ߣ�
�䷽��Ϊy2=4x��
��2���⣺��ֱ��MA��б��Ϊk��k��0������MA����ֱ�߷���Ϊy=kx��
����ֱ��MA�������߷��̣���$A��\frac{4}{k^2}��\frac{4}{k}��$��
���������NA�ķ���Ϊ$\frac{4}{k}y=4•\frac{{x+\frac{4}{k^2}}}{2}$������������$y=\frac{k}{2}x+\frac{2}{k}$����
��MA��MB����${k_{OB}}=-\frac{1}{k}$��
��ֱ��MB�ķ���Ϊ$y=-\frac{1}{k}x$��
����ֱ��MB�������߷��̣����B��4k2��-4k����
������NB�ķ���Ϊ$-4ky=4•\frac{{x+4{k^2}}}{2}$������������$y=-\frac{1}{2k}x-2k$����
��-�ڵã�$��\frac{k}{2}+\frac{1}{2k}��x+2��\frac{1}{k}+k��=0$�����x=-4����ֵ����
�ʵ�N�Ĺ켣Ϊx=-4���Ǵ�ֱx���һ����ֱ�ߣ�
��3��֤�����ɣ�2����$N��-4��\frac{2}{k}-2k��$��
��${k_{NM}}=\frac{{{k^2}-1}}{2k}$��${k_{AB}}=\frac{{-2pk-\frac{2p}{k}}}{{2p{k^2}-\frac{2p}{k^2}}}=\frac{k}{{1-{k^2}}}$��
��${k_{NM}}•{k_{AB}}=-\frac{1}{2}$����ֵ����
���� ��С����Ҫ���������ߵ����ʣ�ֱ����Բ���ߵ��ۺ�Ӧ�������������漰�������߱����̵���ȡ��ֱ����Բ���ߵ����֪ʶ�Լ�Բ�����ж�ֵ����ȡ����С��Կ����Ļ�����ת��˼�롢��������������кܸ�Ҫ����ѹ���⣮

 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�| A�� | $\frac{3}{4}$ | B�� | $\frac{5}{7}$ | C�� | $\frac{4}{7}$ | D�� | $\frac{9}{4}$ |
| A�� | $\frac{1}{2}$��1-2${\;}^{-\frac{1}{16}}$��-1 | B�� | ��1-2${\;}^{-\frac{1}{16}}$��-1 | C�� | 1-2${\;}^{-\frac{1}{16}}$ | D�� | $\frac{1}{2}$��1-2${\;}^{-\frac{1}{16}}$�� |
| A�� | ����n=k��k��N��ʱ�����������xk+yk�ܱ�x+y���� | |
| B�� | ����n��k��k��N��ʱ�����������xk+yk�ܱ�x+y���� | |
| C�� | ����n=2k+1��k��N*��ʱ�����������x2k+1+y2k+1�ܱ�x+y���� | |
| D�� | ����n=2k-1��k��N*��ʱ�����������x2k-1+y2k-1�ܱ�x+y���� |
| A�� | M2��2n+1 | B�� | ��n��2ʱ��2M��4n-2 | C�� | M2��2n+1 | D�� | ��n��3ʱ��2M��2n+2 |
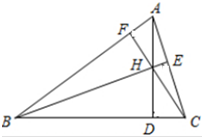 ��ͼ����֪��ABC����������AD��BE��CF������������֤����AD��BE��CF�ཻ��һ�㣮
��ͼ����֪��ABC����������AD��BE��CF������������֤����AD��BE��CF�ཻ��һ�㣮 ��ͼ����������̨ABCD-A1B1C1D1�У�A1B1=a��AB=2a��AA1=$\sqrt{2}a$��E��F�ֱ���AD��AB���е㣮
��ͼ����������̨ABCD-A1B1C1D1�У�A1B1=a��AB=2a��AA1=$\sqrt{2}a$��E��F�ֱ���AD��AB���е㣮