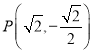题目内容
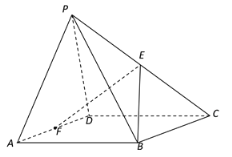
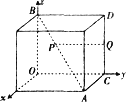
【题目】如图,在棱长为2的正方体中,点P在正方体的对角线AB上,点Q在正方体的棱CD上,若P为动点,Q为动点,则PQ的最小值为_____.

【答案】![]()
【解析】
建立空间直角坐标系,利用![]() 三点共线设出点P(λ,λ,2﹣λ),0≤λ≤2,以及Q(0,2,μ),0≤μ≤2,根据两点间的距离公式,以及配方法,即可求解.
三点共线设出点P(λ,λ,2﹣λ),0≤λ≤2,以及Q(0,2,μ),0≤μ≤2,根据两点间的距离公式,以及配方法,即可求解.
建立如图所示空间直角坐标系,设P(λ,λ,2﹣λ),
Q(0,2,μ)(0≤λ≤2且0≤μ≤2),
可得PQ=![]() ,
,
∵2(λ﹣1)2≥0,(2﹣λ﹣μ)2≥0,∴2(λ﹣1)2+(2﹣λ﹣μ)2+2≥2,
当且仅当λ﹣1=2﹣λ﹣μ=0时,等号成立,此时λ=μ=1,
∴当且仅当PQ分别为ABCD的中点时,
PQ的最小值为![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目