题目内容
已知函数y=2sin（ωx+φ）满足f（-x）=f（x），其图象与直线y=2的某两个交点横坐标为x1，x2，|x1-x2|的最小值为π，则
- A.
，
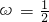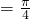
- B.ω=2，
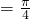
- C.，
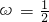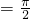
- D.ω=2，
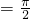
D
分析：由y=2sin（ωx+φ）是偶函数，结合所给的选项可得 φ=
．再由函数的周期为π，即 
=π，求得ω=2，从而得出结论．
解答：∵函数y=2sin（ωx+φ）满足f（-x）=f（x），∴函数y=2sin（ωx+φ）是偶函数，结合所给的选项可得 φ=．
再由其图象与直线y=2的某两个交点横坐标为x1，x2，|x1-x2|的最小值为π，可得函数的周期为π，即=π，故ω=2，
故选D．
点评：本题主要考查利用y=Asin（ωx+φ）的图象特征，由函数y=Asin（ωx+φ）的部分图象求解析式，属于中档题．
分析：由y=2sin（ωx+φ）是偶函数，结合所给的选项可得 φ=
．再由函数的周期为π，即 =π，求得ω=2，从而得出结论．解答：∵函数y=2sin（ωx+φ）满足f（-x）=f（x），∴函数y=2sin（ωx+φ）是偶函数，结合所给的选项可得 φ=
．再由其图象与直线y=2的某两个交点横坐标为x1，x2，|x1-x2|的最小值为π，可得函数的周期为π，即
=π，故ω=2，故选D．
点评：本题主要考查利用y=Asin（ωx+φ）的图象特征，由函数y=Asin（ωx+φ）的部分图象求解析式，属于中档题．
练习册系列答案
相关题目
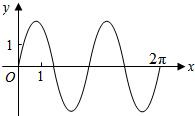已知函数y=2sin（ωx+φ）（ω＞0））在区间[0，2π]的图象如图：那么ω=（ ）| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
已知函数y=2sin（wx+θ）为偶函数，其图象与直线y=2某两个交点的横坐标分别为x1，x2，若|x2-x1|的最小值为π，则该函数在区间（ ）上是增函数．
A、(-
| ||||
B、(-
| ||||
C、(0，
| ||||
D、(
|
下列4个命题：