题目内容
我们把形如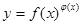 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得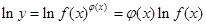 ,两边对
,两边对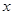 求导数,得
求导数,得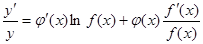 ,于是
,于是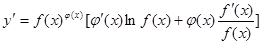 ,运用此方法可以求得函数
,运用此方法可以求得函数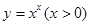 在
在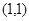 处的切线方程是________________.
处的切线方程是________________.
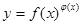 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得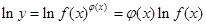 ,两边对
,两边对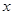 求导数,得
求导数,得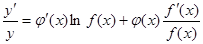 ,于是
,于是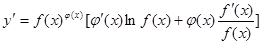 ,运用此方法可以求得函数
,运用此方法可以求得函数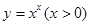 在
在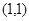 处的切线方程是________________.
处的切线方程是________________.y=x
试题分析:由题目给定的方法可知,
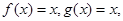 所以
所以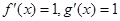 ,
,所以,
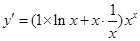 ,所以∴
,所以∴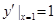 ,即:函数
,即:函数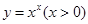 在(1,1)处的切线的斜率为1,故切线方程为:y-1=x-1,即y=x.
在(1,1)处的切线的斜率为1,故切线方程为:y-1=x-1,即y=x.点评:仔细分析题意,找出f(x),g(x),然后依据题意求函数的导数,利用导数的几何意义,求出切线方程即可.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线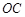 是以直线
是以直线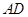 为对称轴,以线段
为对称轴,以线段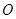 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
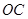 的方程;
的方程;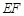 ,使得剩余部分即直角梯形
,使得剩余部分即直角梯形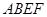 的面积最大?
的面积最大?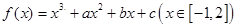 ,且函数
,且函数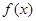 在
在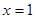 和
和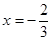 处都取得极值。
处都取得极值。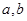 的值;
的值;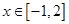 ,
,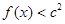 恒成立,求实数
恒成立,求实数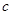 的取值范围。
的取值范围。 (
(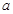 为实常数)。
为实常数)。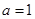 时,求函数
时,求函数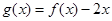 的单调区间;
的单调区间;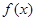 在区间
在区间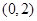 上无极值,求
上无极值,求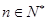 且
且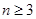 ,求证:
,求证: 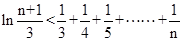 .
.
 的解析式及减区间;
的解析式及减区间;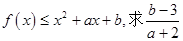 的最小值。
的最小值。 ,
, ,且
,且 ,则
,则 与
与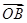 夹角的取值范围是 .
夹角的取值范围是 .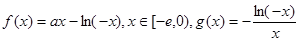 ,其中
,其中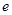 是自然对数的底数,
是自然对数的底数,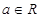
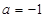 时,
时,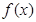 的单调性。
的单调性。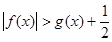
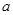 ,使
,使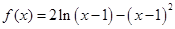 .
.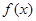 的单调递增区间;
的单调递增区间;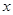 的方程
的方程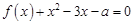 在区间
在区间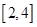 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数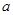 的取值范围.
的取值范围.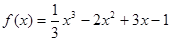 的单调递增区间为____________.
的单调递增区间为____________.