题目内容
如图,有一边长为2米的正方形钢板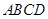 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线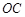 是以直线
是以直线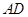 为对称轴,以线段
为对称轴,以线段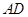 的中点
的中点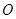 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.

(Ⅰ)请建立适当的直角坐标系,求阴影部分的边缘线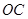 的方程;
的方程;
(Ⅱ)如何画出切割路径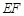 ,使得剩余部分即直角梯形
,使得剩余部分即直角梯形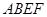 的面积最大?
的面积最大?
并求其最大值.
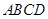 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线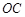 是以直线
是以直线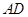 为对称轴,以线段
为对称轴,以线段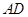 的中点
的中点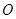 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
(Ⅰ)请建立适当的直角坐标系,求阴影部分的边缘线
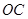 的方程;
的方程;(Ⅱ)如何画出切割路径
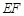 ,使得剩余部分即直角梯形
,使得剩余部分即直角梯形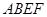 的面积最大?
的面积最大?并求其最大值.
(I) 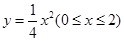 .(Ⅱ)当
.(Ⅱ)当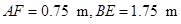 时,可使剩余的直角梯形的面积最大,其最大值为
时,可使剩余的直角梯形的面积最大,其最大值为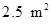 .
.
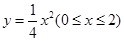 .(Ⅱ)当
.(Ⅱ)当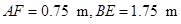 时,可使剩余的直角梯形的面积最大,其最大值为
时,可使剩余的直角梯形的面积最大,其最大值为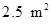 .
. 试题分析:(I)以
 为原点,直线
为原点,直线 为
为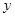 轴,建立如图所示的直角坐标系,
轴,建立如图所示的直角坐标系,
依题意
可设抛物线弧
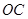 的方程为
的方程为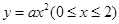
∵点
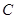 的坐标为
的坐标为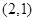 , ∴
, ∴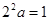 ,
,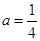
故边缘线
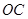 的方程为
的方程为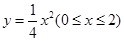 .
.(Ⅱ)要使梯形
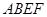 的面积最大,则
的面积最大,则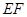 所在的直线必与抛物线弧
所在的直线必与抛物线弧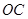 相切,设切点坐标为
相切,设切点坐标为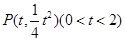 , ∵
, ∵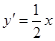 ,
,∴直线
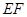 的的方程可表示为
的的方程可表示为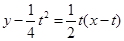 ,即
,即 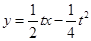 , 由此可求得
, 由此可求得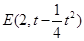 ,
,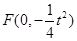 .
.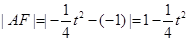 ,
, 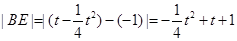 ,
,设梯形
 的面积为
的面积为 ,则
,则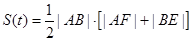
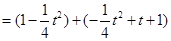
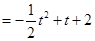
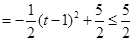 . ∴当
. ∴当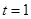 时,
时,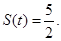
故
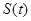 的最大值为
的最大值为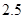 . 此时
. 此时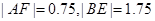 .
. 答:当
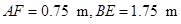 时,可使剩余的直角梯形的面积最大,其最大值为
时,可使剩余的直角梯形的面积最大,其最大值为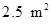 .
. 点评:解应用题常用的方法是依据题意建立等量关系,构造数学模型利用函数的性质进行求解,而有些应用题有明显的几何意义,可以考虑利用解析法根据题意建立适当的坐标系,构造曲线方程,利用曲线的性质进行求解.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 .(Ⅰ) 求
.(Ⅰ) 求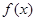 在
在 上的最小值;(Ⅱ) 若存在
上的最小值;(Ⅱ) 若存在 (
( 是常数,
是常数, )使不等式
)使不等式 成立,求实数
成立,求实数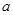 的取值范围;
的取值范围; 都有
都有 成立.
成立. .
. 时,求证:函数
时,求证:函数 在
在 上单调递增;
上单调递增; 有三个零点,求
有三个零点,求 的值.
的值.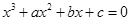 的三个实根分别为一个椭圆,一个抛物线,一个双曲线的离心率,则
的三个实根分别为一个椭圆,一个抛物线,一个双曲线的离心率,则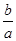 的取值范围________
的取值范围________ 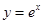 在点
在点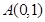 处的切线斜率为 .
处的切线斜率为 .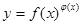 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得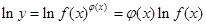 ,两边对
,两边对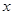 求导数,得
求导数,得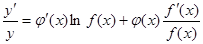 ,于是
,于是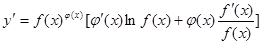 ,运用此方法可以求得函数
,运用此方法可以求得函数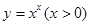 在
在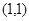 处的切线方程是________________.
处的切线方程是________________.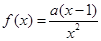 ,其中
,其中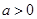 .
.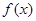 的单调区间;
的单调区间;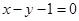 是曲线
是曲线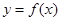 的切线,求实数
的切线,求实数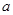 的值;
的值;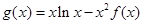 ,求
,求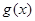 在区间
在区间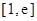 上的最大值.(其中
上的最大值.(其中 为自然对数的底数)
为自然对数的底数) 是定义在R上的奇函数,且f(2)=0,当x>0时,有
是定义在R上的奇函数,且f(2)=0,当x>0时,有 的导数<0恒成立,则不等式
的导数<0恒成立,则不等式 的解集是:
的解集是: (2,+
(2,+  )
)