题目内容
【题目】已知函数 ![]() .
.
(1)求不等式 ![]() 的解集;
的解集;
(2)若关于 ![]() 的不等式
的不等式 ![]() 的解集为
的解集为 ![]() ,求实数
,求实数 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:∵不等式 ![]() ,即
,即 ![]() ,
,
∴① 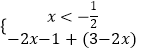 ,或②
,或② 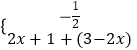 ,或③
,或③ 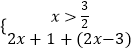 ,
,
解①得: ![]() ;解②得:
;解②得: ![]() ;解③得:
;解③得: ![]() .
.
即不等式的解集为 ![]() .
.
(2)解:∵ ![]() .
.
即 ![]() 的最小值等于4.
的最小值等于4.
∵关于 ![]() 的不等式
的不等式 ![]() 的解集为
的解集为 ![]() ,∴
,∴ ![]() ,解此不等式得:
,解此不等式得: ![]() ,
,
故实数 ![]() 的取值范围是
的取值范围是 ![]() .
.
【解析】对于(1),解含两个绝对值的不等式,往往通过分区间讨论去掉绝对值得到一般不等式求解。
对于(2)不等式解集为空集,往往转化为恒成立或恒不成立来解决。一般会出现最值进行比较。
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
【题目】为了解某社区居民购买水果和牛奶的年支出费用与购买食品的年支出费用的关系,随机调查了该社区5户家庭,得到如下统计数据表:
购买食品的年支出费用x(万元) | 2.09 | 2.15 | 2.50 | 2.84 | 2.92 |
购买水果和牛奶的年支出费用y(万元) | 1.25 | 1.30 | 1.50 | 1.70 | 1.75 |
根据上表可得回归直线方程 ![]() ,其中
,其中 ![]() ,据此估计,该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为( )
,据此估计,该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为( )
A.1.79万元
B.2.55万元
C.1.91万元
D.1.94万元