题目内容
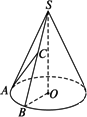
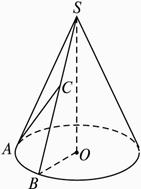
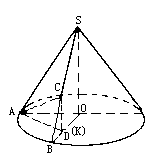
设SA,SB是圆锥SO的两条母线,O是底面圆心,底面半径为10cm,C是SB上一点.(1)求证:AC与平面SOB不垂直;(2)若∠AOB=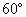 ,C是SB的中点,AC与底面成
,C是SB的中点,AC与底面成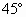 角,求这圆锥的体积.
角,求这圆锥的体积.
答案:
解析:
解析:
|
解(1)假设AC⊥平面SOB,又∵SO⊥平面AOB,∴平面SOB⊥平面AOB,且平面SOB∩平面AOB=OB.在底面内,过A作AD⊥OB于D,∴AD⊥平面SOB,∴AD∥AC.此与AC,AD相交于A矛盾,因此假设不成立,故AC与面SOB不垂直. (2)过C作CK⊥OB于K,则CK⊥平面AOB.∵C是SB的中点,∴K也是OB中点.连AK,则AK⊥OB,又AO=OB=10cm,AC与面AOB成 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
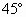 角,∴CK=AK=
角,∴CK=AK= ·10=
·10=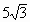 ,又SO=2CK=
,又SO=2CK=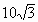 ,∴V=
,∴V=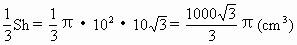 .
.