题目内容
已知双曲线 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率为
的焦点重合,且双曲线的离心率为 ,则此双曲线的方程为
,则此双曲线的方程为
A. | B. | C.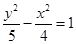 | D. |
D
解析试题分析:根据题意,由于双曲线 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,而抛物线的焦点为(-1,0),c="1," 且双曲线的离心率为
的焦点重合,而抛物线的焦点为(-1,0),c="1," 且双曲线的离心率为 ,故可知
,故可知 ,因此可知
,因此可知 ,故可知双曲线方程为
,故可知双曲线方程为 ,选D.
,选D.
考点:双曲线与抛物线
点评:主要是考查了圆锥曲线的性质的运用,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B. |
C. | D. |
圆心在抛物线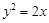 上,且与该抛物线的准线和
上,且与该抛物线的准线和 轴都相切的圆的方程是( )
轴都相切的圆的方程是( )
A.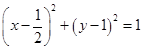 | B.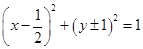 |
C.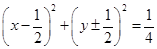 | D.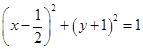 |
椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点,今有一个水平放置的椭圆形台球盘,点 、
、 是它的焦点,长轴长为
是它的焦点,长轴长为 ,焦距为
,焦距为 ,静放在点
,静放在点 的小球(小球的半径不计),从点
的小球(小球的半径不计),从点 沿直线出发,经椭圆壁反弹后第一次回到点
沿直线出发,经椭圆壁反弹后第一次回到点 时,小球经过的路程是( )
时,小球经过的路程是( )
A. | B. | C. | D.以上答案均有可能 |
设椭圆C: 的左、右焦点分别为
的左、右焦点分别为 、
、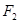 ,P是C上的点,
,P是C上的点, ⊥
⊥
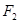 ,
,
∠ =
= ,则C的离心率为( )
,则C的离心率为( )
A. | B. | C. | D.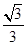 |
 ,在y轴上截得线段长为2
,在y轴上截得线段长为2 .圆心C的轨迹方程是
.圆心C的轨迹方程是



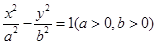 的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若
的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若 ,则双曲线的离心率是
,则双曲线的离心率是 B、
B、 C、
C、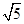 D、
D、
 和
和 轴正方向交点为A,和
轴正方向交点为A,和 轴正方向的交点为B,P为第一象限内椭圆上的点,使四边形OAPB面积最大(O为原点),那么四边形OAPB面积最大值为( )
轴正方向的交点为B,P为第一象限内椭圆上的点,使四边形OAPB面积最大(O为原点),那么四边形OAPB面积最大值为( )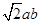



 的左、右焦点,P为直线
的左、右焦点,P为直线 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )


