题目内容
【题目】已知函数
，则满足
恒成立的
的取值个数为（ ）
A. 0B. 1C. 2D. 3
【答案】B
【解析】
由f（x）＝（ex﹣a）（x+a2）≥0，对a分类讨论，可知a≤0时不合题意，当a＞0时， f（x）的两个因式同正同负，则需在同一x处等0，则转化为﹣a2＝lna的根的个数求解．
解：f（x）＝（ex﹣a）（x+a2）≥0，
当a＝0时，f（x）＝（ex﹣a）（x+a2）≥0化为exx≥0，则x≥0，与x∈R矛盾；
当a＜0时，ex﹣a＞0，则x+a2≥0，得x≥﹣a2，与x∈R矛盾；
当a＞0时，令f（x）＝0，得x＝lna或x＝﹣a2，要使f（x）≥0恒成立，
则﹣a2＝lna，作出函数g（a）＝﹣a2与h（a）＝lna的图象如图：
由图可知，a的取值个数为1个．
故选：B．
【题目】为了选拔学生参加全市中学生物理竞赛，学校先从高三年级选取60名同学进行竞赛预选赛，将参加预选赛的学生成绩（单位：分）按范围
，
，
，
分组，得到的频率分布直方图如图：
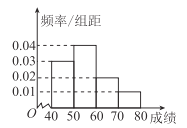
（1）计算这次预选赛的平均成绩（同一组中的数据用该组区间的中点值作代表）；
（2）若对得分在前
的学生进行校内奖励，估计获奖分数线；
（3）若这60名学生中男女生比例为
，成绩不低于60分评估为“成绩良好”，否则评估为“成绩一般”，试完成下面
列联表，是否有
的把握认为“成绩良好”与“性别”有关？
成绩良好 | 成绩一般 | 合计 | |
男生 | |||
女生 | |||
合计 |
附：
，
临界值表：
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
【题目】随着电子阅读的普及，传统纸质媒体遭受到了强烈的冲击．某杂志社近9年来的纸质广告收入如表所示：
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
时间代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
广告收入y（千万元） | 2 | 2.2 | 2.5 | 2.8 | 3 | 2.5 | 2.3 | 2 | 1.8 |
根据这9年的数据，对t和y作线性相关性检验，求得样本相关系数的绝对值为0.243；根据后5年的数据，对t和y作线性相关性检验，求得样本相关系数的绝对值为0.984．
（Ⅰ）如果要用线性回归方程预测该杂志社2019年的纸质广告收入，现在有两个方案，
方案一：选取这9年数据进行预测；方案二：选取后5年数据进行预测．
从实际生活背景以及线性相关性检验的角度分析，你觉得哪个方案更合适？
附：
相关性检验的临界值表：
n-2 | 小概率 | |
0.05 | 0.01 | |
3 | 0.878 | 0.959 |
7 | 0.666 | 0.798 |
（Ⅱ）某购物网站同时销售某本畅销书籍的纸质版本和电子书，某班级有五名同学在该网站购买了这本书，其中三人只购买了电子书，另两人只购买了纸质书，从这五人中任取两人，求两人都购买了电子书的概率．
