题目内容
(本小题满分12分)已知数列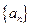 的前
的前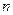 项和是
项和是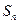 ,且
,且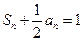 .
.
(Ⅰ)求数列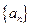 的通项公式;
的通项公式;
(Ⅱ)设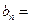
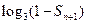 ,求适合方程
,求适合方程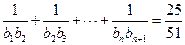 的
的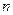 的值.
的值.
(Ⅲ)记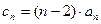 ,是否存在实数M,使得对一切
,是否存在实数M,使得对一切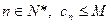 恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
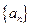 的前
的前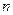 项和是
项和是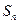 ,且
,且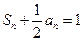 .
.(Ⅰ)求数列
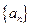 的通项公式;
的通项公式;(Ⅱ)设
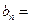
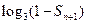 ,求适合方程
,求适合方程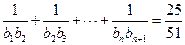 的
的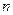 的值.
的值.(Ⅲ)记
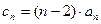 ,是否存在实数M,使得对一切
,是否存在实数M,使得对一切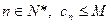 恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
恒成立,若存在,请求出M的最小值;若不存在,请说明理由。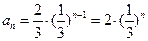 ,
, 2/9
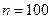
19. 解:(Ⅰ)当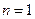 时,
时,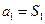 ,由
,由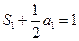 ,得
,得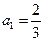 .
.
当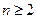 时,
时,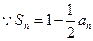 ,
, ,∴
,∴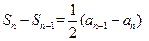 ,
,
即 .∴
.∴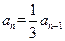 .∴
.∴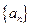 是以
是以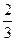 为首项,
为首项,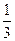 为公比的等比数列.
为公比的等比数列.
故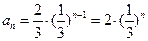 . ………………6分
. ………………6分
(Ⅱ)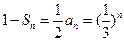 ,
,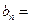
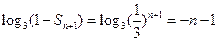 ,………………8分
,………………8分
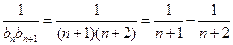
 ………10分
………10分
解方程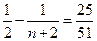 ,得
,得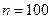 ………………12分
………………12分
(2)解法一: ,
,
由错误!不能通过编辑域代码创建对象。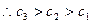 ,
,
当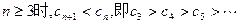 , 又
, 又
故存在实数M,使得对一切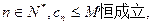 M的最小值为2/9。
M的最小值为2/9。
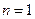 时,
时,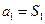 ,由
,由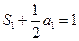 ,得
,得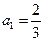 .
. 当
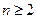 时,
时,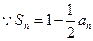 ,
, ,∴
,∴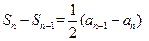 ,
,即
 .∴
.∴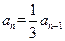 .∴
.∴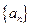 是以
是以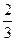 为首项,
为首项,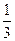 为公比的等比数列.
为公比的等比数列.故
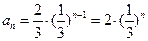 . ………………6分
. ………………6分(Ⅱ)
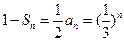 ,
,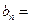
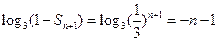 ,………………8分
,………………8分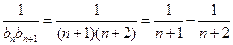
 ………10分
………10分解方程
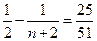 ,得
,得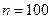 ………………12分
………………12分(2)解法一:
 ,
,由错误!不能通过编辑域代码创建对象。
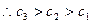 ,
,当
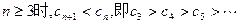 , 又
, 又
故存在实数M,使得对一切
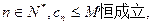 M的最小值为2/9。
M的最小值为2/9。
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
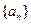 为等比数列,Sn是它的前n项和。若
为等比数列,Sn是它的前n项和。若 , 且
, 且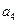 与2
与2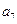 的等差中项为
的等差中项为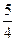 ,则
,则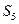 =
=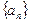 中,已知
中,已知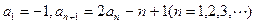 .
.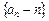 是等比数列;
是等比数列;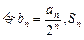 为数列
为数列 的前
的前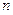 项和,求
项和,求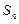 的表达式.
的表达式. 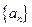 的前n项和为
的前n项和为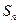 ,且
,且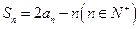 .
.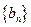 中,
中,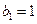 ,点P(
,点P(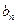 ,
,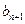 )在直线
)在直线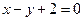 上,记
上,记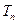 ,当
,当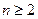 时,试比较
时,试比较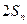 与
与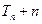 的大小.
的大小.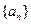 和
和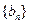 满足
满足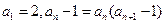 ,
,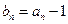 ,数列
,数列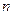 和为
和为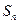 .
. (2)设
(2)设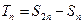 ,求证:
,求证: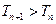 ;
;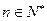 有
有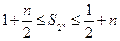 成立.
成立.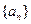 满足
满足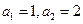 且
且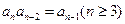 ,则
,则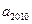 的值为
的值为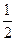
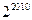
 次。规定:第一只羊报出的数为
次。规定:第一只羊报出的数为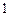 ,第二只羊报出的数为
,第二只羊报出的数为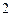 ,之后每只羊所报出的数都是前两只羊所报出的数之和;若报出的数是
,之后每只羊所报出的数都是前两只羊所报出的数之和;若报出的数是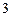 的倍数,则报该数的羊得
的倍数,则报该数的羊得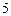 分,若报出的数不是
分,若报出的数不是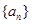 是公差不为0的等差数列,且
是公差不为0的等差数列,且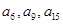 依次为等比数列
依次为等比数列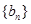 的连续三项,若数列
的连续三项,若数列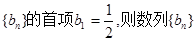 的前5项和S5等于 。
的前5项和S5等于 。