题目内容
已知数列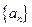 的前n项和为
的前n项和为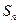 ,且
,且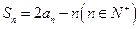 .
.
(1)求数列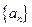 的通项;
的通项;
(2)若数列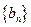 中,
中,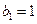 ,点P(
,点P(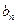 ,
,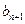 )在直线
)在直线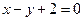 上,记
上,记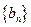 的前n项和为
的前n项和为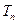 ,当
,当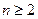 时,试比较
时,试比较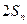 与
与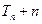 的大小.
的大小.
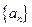 的前n项和为
的前n项和为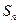 ,且
,且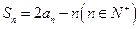 .
.(1)求数列
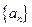 的通项;
的通项;(2)若数列
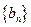 中,
中,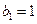 ,点P(
,点P(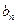 ,
,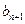 )在直线
)在直线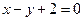 上,记
上,记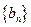 的前n项和为
的前n项和为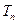 ,当
,当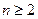 时,试比较
时,试比较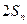 与
与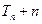 的大小.
的大小.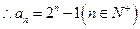 ,当
,当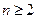 时,
时,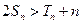
(1)解: 已知
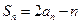 ①
①当
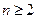 时,
时,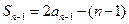 ②
②②-①得

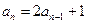 ………………………(2分)
………………………(2分) 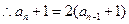 又
又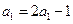
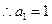
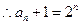
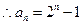 …(4分)
…(4分)由于
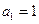 也适合上式,所以
也适合上式,所以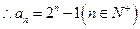 …………(6分)
…………(6分)(2)点P(
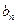 ,
,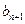 )在直线
)在直线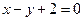 上,所以
上,所以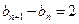 ,
,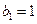 ,所以
,所以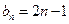 ,
,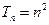 .…………(8分)
.…………(8分)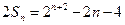
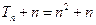 当
当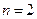 时,
时,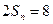 ,
,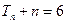 ,
,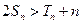 .…………(9分)
.…………(9分)下证当
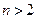 时,
时,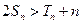
因为
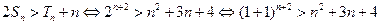
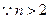 ,
,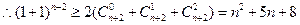
综上可得:当
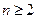 时,
时,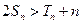 …………(12分)
…………(12分)
练习册系列答案
相关题目
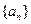 的前n项和为
的前n项和为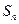 ,且
,且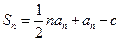 (c是常数,
(c是常数,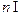 N*),
N*),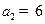 .
.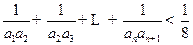 .
.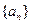 中,
中,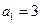 ,
,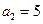 ,其前
,其前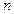 项和
项和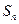 满足
满足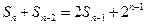
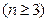 ,令
,令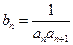 .
.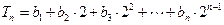 ,求证:
,求证: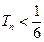 ;
; 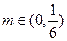 ,均存在
,均存在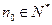 ,使得
,使得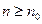 时,
时,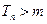 .
.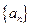 的前
的前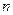 项和是
项和是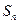 ,且
,且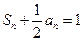 .
.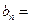
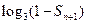 ,求适合方程
,求适合方程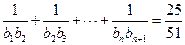 的
的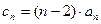 ,是否存在实数M,使得对一切
,是否存在实数M,使得对一切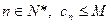 恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
恒成立,若存在,请求出M的最小值;若不存在,请说明理由。 的公差为
的公差为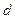 ,且
,且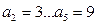 ,数列
,数列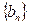 的前
的前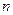 项和为
项和为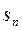 ,且
,且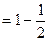
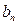
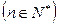

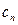 =
=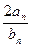 求证:数列
求证:数列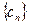 的前
的前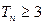 。
。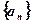 的前
的前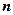 项和
项和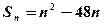 ,
,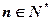 .
.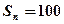 ,求
,求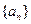 是等差数列,
是等差数列,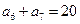 ,
,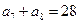 ,则该数列前13项和
,则该数列前13项和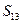 等于
等于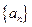 是等差数列,若
是等差数列,若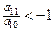 ,且它的前n项和
,且它的前n项和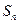 有最大值,那么当
有最大值,那么当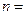 ( )
( )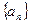 的前
的前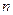 项和为
项和为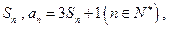 则
则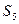 为 。
为 。