题目内容
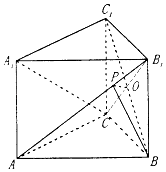
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°.BC=CC1=a,AC=2a. 
(1)求证:AB1⊥BC1;
(2)求二面角B﹣AB1﹣C的正弦值.
【答案】
(1)证明:∵ABC﹣A1B1C1是直三棱柱,
∴CC1⊥平面ABC,则AC⊥CC1.
又∵AC⊥BC,BC∩CC1=C,
∴AC⊥平面B1BCC1,则AC⊥BC1,
∵BC=CC1,∴四边形B1BCC1是正方形,
∴BC1⊥B1C,
又AC∩B1C=C,∴BC1⊥平面AB1C,则AB1⊥BC1
(2)解:设BC1∩B1C=O,作OP⊥AB1于点P,连结BP.
由(1)知BO⊥AB1,而BO∩OP=O,
∴AB1⊥平面BOP,则BP⊥AB1,
∴∠OPB是二面角B﹣AB1﹣C的平面角.
∵△OPB1~△ACB1,∴ ![]() ,
,
∵BC=CC1=a,AC=2a,∴OP= ![]() ,
,
∴ ![]() =
= ![]() .
.
在Rt△POB中,sin∠OPB= 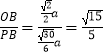 ,
,
∴二面角B﹣AB1﹣C的正弦值为 ![]() .
.
【解析】(1)由已知可得AC⊥平面B1BCC1 , 则AC⊥BC1 , 再由BC=CC1 , 得BC1⊥B1C,由线面垂直的判定可得BC1⊥平面AB1C,从而得到AB1⊥BC1;(2)设BC1∩B1C=O,作OP⊥AB1于点P,连结BP.由(1)知BO⊥AB1 , 进一步得到AB1⊥平面BOP,说明∠OPB是二面角B﹣AB1﹣C的平面角.然后求解直角三角形得答案.

练习册系列答案
相关题目