题目内容
9. 如图,在直三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,
如图,在直三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,(Ⅰ)求证:AC⊥BC1;
(Ⅱ)在AB上是否存在点D使得AC1∥平面CDB1.
分析 (1)根据直线与平面垂直的判定定理证明线面垂直,再利用直线与平面垂直的性质即可证明AC⊥BC1.
(2)利用三角形中位线的性质证明线线平行,再根据直线与平面平行的判定定理即可证明AC1∥平面CDB1.
解答 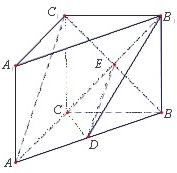 证明:(1)在△ABC中,AC=3,BC=4,AB=5,
证明:(1)在△ABC中,AC=3,BC=4,AB=5,
所以AB2=AC2+BC2,故AC⊥BC.
因为C1C⊥平面ABC,AC?平面ABC,所以AC⊥C1C.
又C1C?平面BB1C1C,BC?平面BB1C1C,且C1C∩BC=C,
所以AC⊥平面BB1C1C.
又BC1?平面BB1C1C,所以AC⊥BC1.
(2)存在点D是AB的中点,使得AC1∥平面CDB1.
证明:设CB1与C1B的交点为E,连结DE,
因为E为正方形CBB1C1对角线的交点,
所以E为C1B的中点.
又D是AB的中点,
所以DE为△ABC1的中位线,
故DE∥AC1.
因为AC1?平面CDB1,DE?平面CDB1,所以AC1∥平面CDB1.
点评 本题考查直线与平面平行的判定定理以及直线与平面垂直的判定定理的应用.属于中档题.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
14.若P(2,1)为圆(x-1)2+y2=36的弦AB的中点,则直线AB的方程是( )
| A. | x-y-3=0 | B. | 2x+y-3=0 | C. | x+y-1=0 | D. | x+y-3=0 |