题目内容
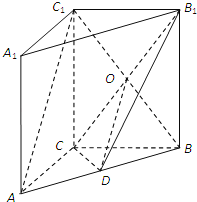
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,点D是AB的中点.求证:

(1)AC⊥BC1;
(2)AC1∥平面B1CD.
【答案】(1)(2)证明见解析
【解析】
试题(1)利用线面垂直的判定定理先证明AC⊥平面BCC1B1,BC1平面BCC1B1,即可证得AC⊥BC1;
(2)取BC1与B1C的交点为O,连DO,则OD是三角形ABC1的中位线,OD∥AC1,而AC1平面B1CD,利用线面平行的判定定理
即可得证.
证明:(1)在直三棱柱ABC﹣A1B1C1中,∵CC1⊥平面ABC,
∴CC1⊥AC,
又AC⊥BC,BC∩CC1=C,
∴AC⊥平面BCC1B1
∴AC⊥BC1.
(2)设BC1与B1C的交点为O,连接OD,BCC1B1为平行四边形,则O为B1C中点,又D是AB的中点,
∴OD是三角形ABC1的中位线,OD∥AC1,
又∵AC1平面B1CD,OD平面B1CD,
∴AC1∥平面B1CD.

练习册系列答案
相关题目

