题目内容
在双曲线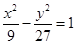 中,F1、F2分别为其左右焦点,点P在双曲线上运动,求△PF1F2的重心G的轨迹方程.
中,F1、F2分别为其左右焦点,点P在双曲线上运动,求△PF1F2的重心G的轨迹方程.
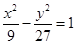 中,F1、F2分别为其左右焦点,点P在双曲线上运动,求△PF1F2的重心G的轨迹方程.
中,F1、F2分别为其左右焦点,点P在双曲线上运动,求△PF1F2的重心G的轨迹方程.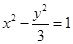 (y≠0)
(y≠0)试题分析:在双曲线
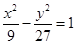 中F1(-6,0),F2(6,0),设点P(m,n ),则
中F1(-6,0),F2(6,0),设点P(m,n ),则 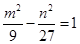 ①.
①.设△PF1F2的重心G(x,y),则由三角形的重心坐标公式可得
x=
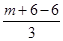 ,y=
,y=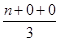 ,即 m=3x,n=3y,代入①化简可得
,即 m=3x,n=3y,代入①化简可得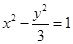 (y≠0)。
(y≠0)。点评:中档题,“相关点法(代入法)”是一种重要的求轨迹方程的方法。

练习册系列答案
相关题目
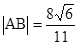 。
。 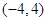 的抛物线的标准方程是
的抛物线的标准方程是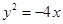
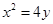
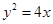 或
或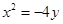
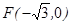 ,且过
,且过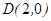 ,设点
,设点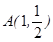 .
.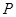 是椭圆上的动点,求线段
是椭圆上的动点,求线段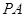 中点
中点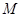 的轨迹方程。
的轨迹方程。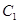 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线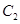 :
: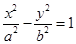 的左焦点
的左焦点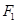 且垂直于
且垂直于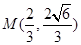 .
.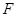 的坐标;
的坐标;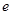 .
.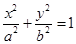 (
(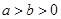 )中,
)中,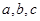 成等比数列,则椭圆的离心率为( )
成等比数列,则椭圆的离心率为( )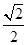
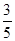
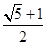
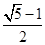
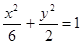 的右焦点重合,则此抛物线的方程是( )
的右焦点重合,则此抛物线的方程是( )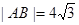 ,则双曲线C的方程为__________.
,则双曲线C的方程为__________.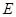 的焦点在
的焦点在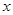 轴上,离心率为
轴上,离心率为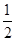 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点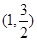 .
.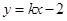 与椭圆
与椭圆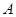 、
、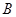 两点,
两点, 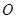 为原点,在
为原点,在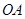 、
、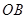 上分别存在异于
上分别存在异于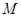 、
、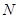 ,使得
,使得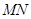 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率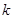 的取值范围.
的取值范围.