题目内容
8.数列{an}的通项公式an=$\frac{3n-2}{3n+1}$.(1)求这个数列的第10项;
(2)$\frac{98}{101}$是不是该数列的项?
(3)判断数列{an}的单调性,并求数列的最大、最小项.
分析 (1)令n=10,可得a10.
(2)假设$\frac{98}{101}$是该数列的项,则$\frac{98}{101}$=$\frac{3n-2}{3n+1}$,解得n是否是正整数,即可判断出是否是该数列的项.
(3)an=$\frac{3n+1-3}{3n+1}$=1-$\frac{3}{3n+1}$.利用数列$\{\frac{3}{3n+1}\}$单调递减,可得数列$\{1-\frac{3}{3n+1}\}$单调递增,即可得出.
解答 解:(1)a10=$\frac{3×10-2}{3×10+1}$=$\frac{28}{31}$.
(2)假设$\frac{98}{101}$是该数列的项,则$\frac{98}{101}$=$\frac{3n-2}{3n+1}$,解得n=$\frac{100}{3}$∉N,因此$\frac{98}{101}$不是该数列的项.
(3)an=$\frac{3n-2}{3n+1}$=$\frac{3n+1-3}{3n+1}$=1-$\frac{3}{3n+1}$.
∵数列$\{\frac{3}{3n+1}\}$单调递减,
∴数列$\{1-\frac{3}{3n+1}\}$单调递增;
∴数列的最小项为a1=$\frac{1}{4}$,无最大项.
点评 本题考查了数列的通项公式、数列的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
19.不等式2x>${(\frac{1}{2})}^{x-x^2}$的解集为( )
| A. | (-∞,0)∪(2,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (0,2) | D. | [0,2] |
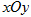 中,点
中,点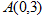 ,直线
,直线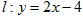 ,设圆
,设圆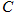 的半径为
的半径为 ,圆心在
,圆心在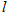 上.
上.
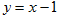 上,过点
上,过点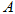 作圆
作圆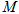 ,使
,使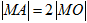 ,求圆心
,求圆心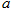 的取值范围.
的取值范围. ,则
,则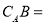 ( )
( )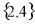 B.
B.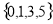 C.
C.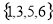 D.
D.