题目内容
20.二次函数f(x)的图象的顶点为A(1,16),且图象在x轴上截得的线段长为8.(1)求函数f(x)解析式;
(2)令g(x)=f(x)+(2a-2)x.
①求函数g(x)在x∈[0,2]上的最小值;
②若x∈[0,2]时,不等式g(x)≤17恒成立,试求实数a的取值范围.
分析 (1)根据其顶点坐标用顶点式二次函数通式设抛物线的解析式,然后根据图象在x轴上截得线段长是8,求得图象与x轴交于(-3,0)和(5,0)两点,代入抛物线中即可求得二次函数的解析式;
(2)先求出函数的解析式,确定函数的对称轴,再结合函数的定义域进行分类讨论,一元二次函数的性质分别求出g(x)在区间[0,2]上的最大值和最小值即可.
解答 解:(1)∵二次函数f(x)的图象顶点为A(1,16),
∴设二次函数解析式为f(x)=a(x-1)2+16.
又∵图象在x轴上截得线段长是8,
∴图象与x轴交于(-3,0)和(5,0)两点.
∴a(-3-1)2+16=0,
∴a=-1,
∴所求二次函数解析式为f(x)=-x2+2x+15.
(2)①g(x)=f(x)+(2a-2)x=(2a-2)x+f(x)=(2a-2)x+(-x2+2x+15)=-x2+2ax+15=-(x-a)2+a2+15.
对称轴为x=a,
若a≤0时,g(x)在区间[0,2]上为单调减函数,∴g(x)的最小值g(2)=11+4a.
1<a<2时,g(x)在区间[0,a]上为单调递增函数,在[a,2]上为单调减函数,
∴x=0时,取得最小值,最小值g(0)=15;
0≤a≤1,时,g(x)在区间[0,a]上为单调增函数,在[a,2]上为单调减函数,
∴当x=2时,取得最小值g(2)=11+4a;
a≥2时,g(x)在区间[0,2]上为单调增函数,∴x=0时,g(x)取得最小值g(0)=15,
即函数g(x)在x∈[0,2]上的最小值为y=$\left\{\begin{array}{l}{11+4a,}&{a≤1}\\{15,}&{a>1}\end{array}\right.$.
②若x∈[0,2]时,不等式g(x)≤17恒成立,
等价为g(x)max≤17恒成立.
若a≤0时,g(x)在区间[0,2]上为单调减函数,∴g(x)的最大值g(0)=15.
若a≥2时,g(x)在区间[0,2]上为单调增函数,∴x=2时,g(x)取得最大值g(2)=11+4a;
若0<a<2时,g(x)在区间[0,a]上为单调递增函数,在[a,2]上为单调减函数,
∴x=a时,取得最大值,最大值g(a)=a2+15;
即此时函数的最大值为y=$\left\{\begin{array}{l}{15,}&{a≤0}\\{{a}^{2}+15,}&{0<a<2}\\{11+4a,}&{a≥2}\end{array}\right.$.
若a≤0,则15≤17成立,
若0<a<2,由a2+15≤17得a2≤2,解得-$\sqrt{2}$≤a≤$\sqrt{2}$,此时0<a≤$\sqrt{2}$,
若a≥2,则由11+4a≤17得4a≤6,解得a≤$\frac{3}{2}$,此时不成立,
综上a≤$\sqrt{2}$.
点评 本题重点考查函数的解析式,考查函数的最值,解题的关键是利用待定系数法假设方程,利用函数对称轴与定义域的关系,合理进行分类讨论.

 阅读快车系列答案
阅读快车系列答案| A. | 16 | B. | 128 | C. | 32 | D. | 64 |
| A. | (-∞,1)∪(1,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (-∞,0),(0,+∞) | D. | (-∞,1),(1,+∞) |
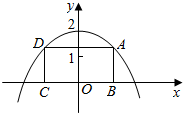 如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.
如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.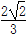 ,a=2,该三角形的面积为
,a=2,该三角形的面积为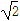 ,则b的值为( )
,则b的值为( ) B.
B. 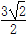 C.2
C.2