题目内容
1.若直线y=a与函数y=|$\frac{lnx+1}{{x}^{3}}$|的图象恰有3个不同的交点,则实数a的取值范围为( )| A. | {$\frac{{e}^{2}}{3}$} | B. | (0,$\frac{{e}^{2}}{3}$) | C. | ($\frac{{e}^{2}}{3}$,e) | D. | ($\frac{1}{e}$,1)∪{$\frac{{e}^{2}}{3}$} |
分析 先求得函数y=|$\frac{lnx+1}{{x}^{3}}$|的定义域为(0,+∞),再分段y=|$\frac{lnx+1}{{x}^{3}}$|=$\left\{\begin{array}{l}{\frac{-lnx-1}{{x}^{3}},x∈(0,{e}^{-1})}\\{\frac{lnx+1}{{x}^{3}},x∈[{e}^{-1},+∞)}\end{array}\right.$,从而分别求导确定函数的单调性,从而解得.
解答 解:函数y=|$\frac{lnx+1}{{x}^{3}}$|的定义域为(0,+∞),
y=|$\frac{lnx+1}{{x}^{3}}$|=$\left\{\begin{array}{l}{\frac{-lnx-1}{{x}^{3}},x∈(0,{e}^{-1})}\\{\frac{lnx+1}{{x}^{3}},x∈[{e}^{-1},+∞)}\end{array}\right.$,
当x∈(0,e-1)时,y′=$\frac{3lnx+2}{{x}^{4}}$,
∵x∈(0,e-1),∴lnx<-1,
∴y′=$\frac{3lnx+2}{{x}^{4}}$<0,
∴y=|$\frac{lnx+1}{{x}^{3}}$|在(0,e-1)上是减函数;
当x∈(e-1,+∞)时,y′=-$\frac{3lnx+2}{{x}^{4}}$,
∴当x∈(e-1,${e}^{-\frac{2}{3}}$)时,∴y′>0,
当x∈(${e}^{-\frac{2}{3}}$,+∞)时,∴y′<0,
∴y=|$\frac{lnx+1}{{x}^{3}}$|在(e-1,${e}^{-\frac{2}{3}}$)上是增函数,
在(${e}^{-\frac{2}{3}}$,+∞)上是减函数;
且$\underset{lim}{x→{0}^{+}}$|$\frac{lnx+1}{{x}^{3}}$|=+∞,f(e-1)=0,
f(${e}^{-\frac{2}{3}}$)=$\frac{{e}^{2}}{3}$,$\underset{lim}{x→+∞}$|$\frac{lnx+1}{{x}^{3}}$|=0,
故实数a的取值范围为(0,$\frac{{e}^{2}}{3}$),
故选B.
点评 本题考查了导数的综合应用及分段函数的应用.

 名校课堂系列答案
名校课堂系列答案| A. | 0∈A | B. | 1.5∉A | C. | -1∉A | D. | 8∈A |
| A. | (0,1) | B. | (1,+∞) | C. | ($\frac{1}{8}$,1) | D. | (0,$\frac{1}{8}$) |
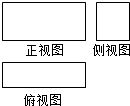 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )| A. | 3$\sqrt{5}$+2 | B. | 6$\sqrt{5}$+4 | C. | 6 | D. | 10 |
| A. | (0,$\frac{1}{2}$] | B. | ($\frac{1}{4}$,$\frac{3}{4}$] | C. | [$\frac{1}{2}$,$\frac{3}{4}$) | D. | [$\frac{1}{4}$,1) |
| A. | 2x+y-5=0 | B. | x-2y=0 | C. | 2x+y-3=0 | D. | x+2y=0 |