题目内容
给定平面上四点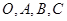 满足
满足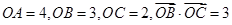 ,则
,则 面积的最大值为
面积的最大值为

解析试题分析:
由已知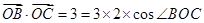 ,得
,得 ,由余弦定理可得
,由余弦定理可得 ,从而
,从而 中边
中边 边上的高为
边上的高为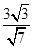 ,由
,由 知点
知点 在以
在以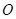 为圆心,4为半径的圆上,
为圆心,4为半径的圆上, 到直线
到直线 的距离最大值为
的距离最大值为 ,∴
,∴ 面积的最大值为
面积的最大值为 .
.
考点:向量的数量积,三角形面积最大值.

练习册系列答案
相关题目
题目内容
给定平面上四点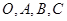 满足
满足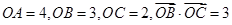 ,则
,则 面积的最大值为
面积的最大值为

解析试题分析:
由已知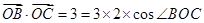 ,得
,得 ,由余弦定理可得
,由余弦定理可得 ,从而
,从而 中边
中边 边上的高为
边上的高为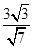 ,由
,由 知点
知点 在以
在以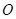 为圆心,4为半径的圆上,
为圆心,4为半径的圆上, 到直线
到直线 的距离最大值为
的距离最大值为 ,∴
,∴ 面积的最大值为
面积的最大值为 .
.
考点:向量的数量积,三角形面积最大值.
