题目内容
7.在梯形ABCD中,AB∥DC,DC=1,AB=2,对角线AC与BD的交点为O,点E在腰AD上,且$\overrightarrow{EO}=λ\overrightarrow{AB}$,则实数λ=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 如图所示,由DC∥AB,可得$\frac{DO}{OB}=\frac{DC}{AB}=\frac{1}{2}$.$\frac{DO}{DB}$=$\frac{1}{3}$.由$\overrightarrow{EO}=λ\overrightarrow{AB}$,可得EO∥AB,$\frac{EO}{AB}=\frac{DO}{DB}$=$\frac{1}{3}$.即可得出.
解答 解:如图所示,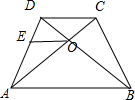
∵DC∥AB,
∴$\frac{DO}{OB}=\frac{DC}{AB}=\frac{1}{2}$.
∴$\frac{DO}{DB}$=$\frac{1}{3}$.
∵$\overrightarrow{EO}=λ\overrightarrow{AB}$,
∴EO∥AB,
∴$\frac{EO}{AB}=\frac{DO}{DB}$=$\frac{1}{3}$.
∴$\overrightarrow{EO}$=$\frac{1}{3}\overrightarrow{AB}$.
∴$λ=\frac{1}{3}$.
故选:A.
点评 本题考查了向量共线定理、平行线分线段成比例定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
17.函数y=$\frac{1}{x+3}$在x∈[-1,1]上的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 2 | D. | 4 |
17.函数y=cos(sin|x|)的图象大致是( )
| A. | 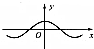 | B. | 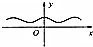 | C. | 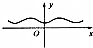 | D. |  |