题目内容
11.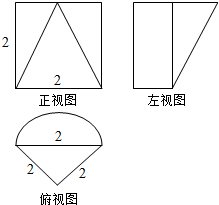 正三棱柱被一个平面截去一部分后与半圆柱组成一个几何体,该几何体的三视图如图所示,则该几何体的表面积为( )
正三棱柱被一个平面截去一部分后与半圆柱组成一个几何体,该几何体的三视图如图所示,则该几何体的表面积为( )| A. | 3π+4+$\sqrt{3}$+$\sqrt{7}$ | B. | 3π+6+$\sqrt{3}$ | C. | 2π+4+$\sqrt{3}$$+\sqrt{7}$ | D. | 2π+6$+\sqrt{3}$ |
分析 根据几何体的三视图,得出该几何体是四棱锥与半圆柱的组合体,结合图中数据求出它的表面积.
解答 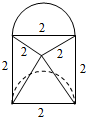 解:根据几何体的三视图,得;
解:根据几何体的三视图,得;
该几何体是四棱锥与半圆柱的组合体,
且四棱锥的底面是边长为2的正方形,侧面有两个全等的等腰直角三角形,
一个边长为2的等边三角形,一个为底面边长是2的等腰三角形,
半圆柱的底面直径为2,高为2,如图所示;
则该几何体的表面积为
S=(2×$\frac{1}{2}$π•12+$\frac{1}{2}$π•2•2)+(2×$\frac{1}{2}$•2•2+$\frac{1}{2}$•22•sin60°+$\frac{1}{2}$•2•$\sqrt{{2}^{2}{+2}^{2}{-1}^{2}}$)
=3π+4+$\sqrt{3}$+$\sqrt{7}$.
故选:A.
点评 本题考查了空间几何体三视图的应用问题,解题的关键是根据三视图得出几何体的结构特征,是基础题目.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
16.某几何体的三视图如图所示,则该几何体的体积可以是( )


| A. | $48+\frac{4}{3}π$ | B. | 48+2π | C. | $48+\frac{8}{3}π$ | D. | 48+3π |
3.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.若实数a满足f(log2a)+f(${log_{\frac{1}{2}}}a$)≤2f(2),则a的取值范围是( )
| A. | (-∞,4] | B. | (0,4] | C. | $(0,\frac{1}{4}]$ | D. | $[\frac{1}{4},4]$ |
20.《九章算术》之后,人们进一步地用等差数列求和公式来解决更多的问题.《张邱建算经》卷上第22题为:今有女善织,日益功疾(注:从第2天起每天比前一天多织相同量的布),第一天织5尺布,现在一月(按30天计),共织390尺布,则第2天织的布的尺数为( )
| A. | $\frac{161}{29}$ | B. | $\frac{161}{31}$ | C. | $\frac{81}{15}$ | D. | $\frac{80}{15}$ |
 如图所示,在直三棱柱ABC-A1B1C1中,BC=AC,AC1⊥A1B,M,N分别是A1B1,AB的中点,给出下列结论:①C1M⊥平面A1ABB1,②A1B⊥NB1,③平面AMC1∥平面CNB1,其中正确结论的个数为( )
如图所示,在直三棱柱ABC-A1B1C1中,BC=AC,AC1⊥A1B,M,N分别是A1B1,AB的中点,给出下列结论:①C1M⊥平面A1ABB1,②A1B⊥NB1,③平面AMC1∥平面CNB1,其中正确结论的个数为( )