题目内容
6.若$\sqrt{9{a}^{2}-6a+1}$=3a-1,则a的取值范围是[$\frac{1}{3}$,+∞).分析 直接利用配方法化简方程,然后求解a的范围.
解答 解:$\sqrt{9{a}^{2}-6a+1}$=|3a-1|=3a-1,
则3a-1≥0,
解得a$≥\frac{1}{3}$.
$\sqrt{9{a}^{2}-6a+1}$=3a-1,则a的取值范围是:[$\frac{1}{3}$,+∞).
故答案为::[$\frac{1}{3}$,+∞).
点评 本题考查方程的思想,根式的运算法则的应用,是基础题.

练习册系列答案
相关题目
17.在数列{an}中,a1=cosθ,an+1=ansinθ,其中0<θ<2π,θ≠$\frac{π}{2}$且θ≠$\frac{3π}{2}$,若$\underset{lim}{n→∞}$(a1+a2+…+an)=$-\frac{\sqrt{3}}{3}$,则θ等于( )
| A. | $\frac{7π}{10}$ | B. | $\frac{5π}{12}$ | C. | $\frac{7π}{6}$ | D. | $\frac{5π}{6}$ |
11.字母N、Z、Q和R分别表示自然数集、整数集、有理数集和实数集,则它们之间的关系是( )
| A. | N?Q?Z?R | B. | N?Z?Q?R | C. | R?Q?Z?N | D. | Z?N?Q?R |
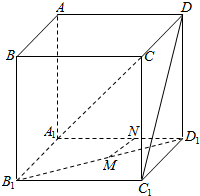 在正方体ABCD-A1B1C1D1中,若M、N分别为B1D1与C1D上的点,且MN⊥B1D,MN⊥C1D1,则MN与A1C的位置关系是MN∥A1C.1.
在正方体ABCD-A1B1C1D1中,若M、N分别为B1D1与C1D上的点,且MN⊥B1D,MN⊥C1D1,则MN与A1C的位置关系是MN∥A1C.1.