题目内容
定义区间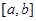 的长度为
的长度为 .若
.若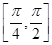 是函数
是函数 的一个长度最大的单调递减区间,则
的一个长度最大的单调递减区间,则
A. , , | B. , , |
C. , , | D. , , |
D
解析试题分析:根据给定的函数,因为已知[ ]是函数的一个长度最大的一个单调递减区间,则说明了周期为
]是函数的一个长度最大的一个单调递减区间,则说明了周期为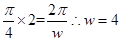 ,因此排除A,B,然后对于C,D来说。由于在该区间是递减的,那么
,因此排除A,B,然后对于C,D来说。由于在该区间是递减的,那么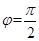 代入解析式中,看是否满足是递减,不满足就舍去,此时可知
代入解析式中,看是否满足是递减,不满足就舍去,此时可知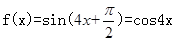 应该是单调递减区间不成立,故排除选D.
应该是单调递减区间不成立,故排除选D.
考点:三角函数性质
点评:本试题考查了基本的三角函数的性质,这部分知识要熟练的掌握,属于基础题。

练习册系列答案
相关题目
函数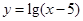 的的定义域是( )
的的定义域是( )
A.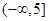 | B.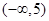 | C.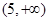 | D.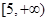 |
定义域为R的函数 满足
满足 ,当
,当 时,
时, ,若
,若 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .
A. | B. |
C. | D. |
函数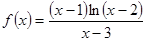 的零点有
的零点有
A. 个 个 | B. 个 个 | C.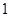 个 个 | D. 个 个 |
已知函数 在
在 上是增函数,
上是增函数, ,若
,若 ,则
,则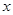 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知 是定义在
是定义在 上的奇函数,且当x<0时不等式
上的奇函数,且当x<0时不等式 成立,若
成立,若 ,
, 
 ,则
,则 大小关系是
大小关系是
A. | B.c > b > a | C. | D.c > a >b |
下列函数在[ ,
, )内为增函数的是( )
)内为增函数的是( )
A. | B. | C. | D. |
函数y= 的定义域是( )
的定义域是( )
| A.[1,+∞) | B.( ,+∞) ,+∞) | C.[ ,1] ,1] | D.( ,1] ,1] |
 的图象为如图所示的折线段
的图象为如图所示的折线段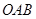 ,其中点
,其中点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 .定义函数
.定义函数 ,则函数
,则函数 的最大值为
的最大值为



