题目内容
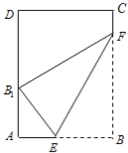
【题目】已知![]() 是复平面内的平行四边形,顶点
是复平面内的平行四边形,顶点![]() ,
,![]() ,
,![]() 对应的复数分别为
对应的复数分别为![]() ,
,![]() ,
,![]() .
.
(1)求点![]() 对应的复数为
对应的复数为![]() ;
;
(2)令复数![]() ,当实数
,当实数![]() 取什么值时,复数
取什么值时,复数![]() 表示的点位于第二或四象限.
表示的点位于第二或四象限.
【答案】(1)![]() = 3+ 2i;(2)
= 3+ 2i;(2)![]()
【解析】
(1)由复数的几何表示将已知复数表示为坐标形式,设D (x, y),进而表示![]() ,由ABCD是平行四边形,即
,由ABCD是平行四边形,即![]() 构建不等式组,解得D点坐标,进而表示复数
构建不等式组,解得D点坐标,进而表示复数![]() ;
;
(2)将已知整理可得z= (m- 2)+(-3m- 4)i,进而表示对应的点坐标,由已知点位于第二或四象限,则横纵坐标乘积为负构建不等式,解得答案.
(1)由已知可得A(1,-3),B(0,-1),C(2,4),设D(x,y),即![]()
因为在复平面内ABCD是平行四边形,即![]() ,则(x-1,y+3)= (2,5),
,则(x-1,y+3)= (2,5),![]()
所以点D的坐标为(3,2)
故![]() =3+2i
=3+2i
(2)将已知整理可得z=(m-2)+(-3m-4)i,m∈R
所以复数z表示的点为(m-2,-3m-4).
由复数![]() 表示的点位于第二或四象限可得(m-2)(-3m-4)<0,即(m-2)(3m+4)>0,
表示的点位于第二或四象限可得(m-2)(-3m-4)<0,即(m-2)(3m+4)>0,
解得m<![]() 或m>2,
或m>2,
故实数m的取值范围是![]() 时,复数z表示的点位于第二、四象限.
时,复数z表示的点位于第二、四象限.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |