Question

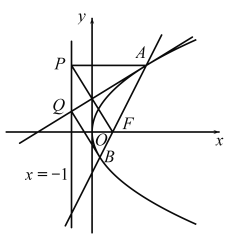
【题目】已知抛物线.

（1）点是该抛物线上任一点，求证：过点的抛物线的切线方程为；

（2）过点作该抛物线的两条切线，切点分别为，，设的面积为，求的最小值.

Answer 1

【答案】（1）证明见解析；（2）4.

【解析】

（1）先确定切线斜率存在，再与抛物线联立，利用判别式为零解得斜率，即得结果；

（2）先根据（1）得两切线方程，再根据过得切点弦方程，利用点到直线距离得高，与抛物线联立，利用弦长公式得底边边长，根据三角形面积公式得，最后根据单调性性质求的最小值.

（1）由于抛物线的对称轴为轴，故切线斜率必存在.

设切线方程为，

，

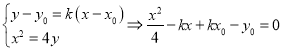，又，

所以，切线方程为，

即.

（2）由（1）可知：切线的方程为，

切线的方程为，

又均过，所以①，②

由①②即知直线的方程为，

，

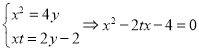
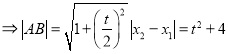又点到直线的距离，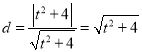

所以，，

等号当且仅当时成立.

故.