题目内容
等比数列 中,
中, ,前
,前 项和为
项和为 ,若数列
,若数列 也为等比数列,则
也为等比数列,则 等于
等于
 中,
中, ,前
,前 项和为
项和为 ,若数列
,若数列 也为等比数列,则
也为等比数列,则 等于
等于 A. | B. | C. | D. |
C
分析:根据数列{an}为等比可设出an的通项公式,因数列{an+1}也是等比数列,进而根据等比性质求得公比q,进而根据等比数列的求和公式求出sn.
解:因数列{an}为等比,则an=2qn-1,
因数列{an+1}也是等比数列,
则(an+1+1)2=(an+1)(an+2+1)
∴an+12+2an+1=anan+2+an+an+2
∴an+an+2=2an+1
∴an(1+q2-2q)=0
∴q=1
即an=2,
所以sn=2n,
故选C.

练习册系列答案
相关题目
 满足
满足
 ,记
,记 ,证明:
,证明: 。
。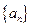 的前
的前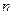 项和是
项和是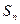 ,且
,且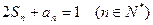 .
.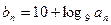 ,求
,求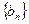 的前
的前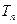 的最大值及相应的
的最大值及相应的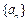 是以a为首项,q为公比的等比数列,
是以a为首项,q为公比的等比数列,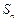 为它的前n项和.
为它的前n项和.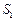 、
、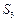 、
、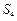 成等差数列时,求q的值;
成等差数列时,求q的值;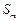 、
、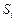 成等差数列时,求证:对任意自然数k,
成等差数列时,求证:对任意自然数k,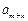 、
、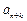 、
、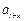 也成等差数列.
也成等差数列. …中的
…中的 等于 ( )
等于 ( )
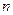 个等式为
个等式为  是公差为-2的等差数列,如果
是公差为-2的等差数列,如果 ,那么
,那么 ( )
( )  B.
B. 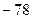 C
C 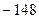 D.
D. 
 是较小的两份之和,则最小1份是( )
是较小的两份之和,则最小1份是( )



 14分)已知数列
14分)已知数列 是以
是以 d为公差的等差数列,数列
d为公差的等差数列,数列 是以q为公比的
是以q为公比的 且
且 ,求整数q的值;
,求整数q的值; ,使得
,使得 项的和?请说明理由;
项的和?请说明理由; ,求证:数列
,求证:数列