题目内容
如图,在直三棱柱ABC-A1B1C1中,已知AB=AC,F为BB1上一点,BF=BC=2,FB1=1,D为BC中点,E为线段AD上不同于点A、D的任意一点.(I)证明:EF⊥FC1;
(II)若AB=
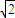 ,求DF与平面FA1C1所成的角.
,求DF与平面FA1C1所成的角.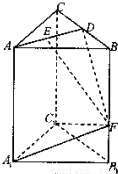
【答案】分析:(1)要证C1F⊥EF,只需证明C1F⊥平面DEF,由AB=AC,,D为BC的中点可得AD⊥BC,由BB1⊥平面ABC 可得BB1⊥AD,由AD⊥平面B1BCC1 可得AD⊥FC1,然后根据已知可证C1F⊥FD,根据线面垂直的判定定理
可得
(2)设DF与平面FA1C1所成的角为θ,点D到FA1C1的距离为h,利用等体积法可求h,由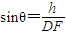 可求
可求
解答:解:(1)AB=AC,,D为BC的中点∴AD⊥BC
∵BB1⊥平面ABC∴BB1⊥AD
∴AD⊥平面B1BCC1∴AD⊥FC1
∵BC=BF=2∴DB=1,又 FB1=1
∴Rt△DBF∽Rt△FB1C1∴ ,
,
∴C1F⊥FD∵FD∩AD=D
∴C1F⊥平面DEF∴C1F⊥EF
(2)设点D到FA1C1的距离为h
由(1)知C1F⊥FD
用等体积法可知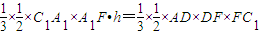
∴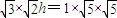 ∴
∴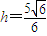
设DF与平面FA1C1所成的角为θ
则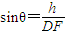 =
=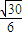
∴DF与平面FA1C1所成的角
点评:本题主要考查了线线垂直与线面垂直的相互转换的应用,而(2)问的求解主要是利用了等体积法求解点到面的距离,这是求解距离的常用方法,避免了做垂线的难点,求而不作.
可得
(2)设DF与平面FA1C1所成的角为θ,点D到FA1C1的距离为h,利用等体积法可求h,由
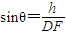 可求
可求解答:解:(1)AB=AC,,D为BC的中点∴AD⊥BC
∵BB1⊥平面ABC∴BB1⊥AD
∴AD⊥平面B1BCC1∴AD⊥FC1
∵BC=BF=2∴DB=1,又 FB1=1
∴Rt△DBF∽Rt△FB1C1∴
 ,
,
∴C1F⊥FD∵FD∩AD=D
∴C1F⊥平面DEF∴C1F⊥EF
(2)设点D到FA1C1的距离为h
由(1)知C1F⊥FD
用等体积法可知
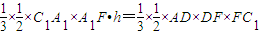
∴
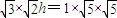 ∴
∴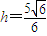
设DF与平面FA1C1所成的角为θ
则
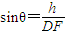 =
=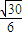
∴DF与平面FA1C1所成的角

点评:本题主要考查了线线垂直与线面垂直的相互转换的应用,而(2)问的求解主要是利用了等体积法求解点到面的距离,这是求解距离的常用方法,避免了做垂线的难点,求而不作.

练习册系列答案
相关题目




