题目内容
如图,在直三棱柱AB-A1B1C1中,∠ BAC=90°,AB=AC=AA1=1,D是棱CC1上一点,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA。

(I)求证:CD=C1D;
(II)求二面角A-A1D-B的平面角的余弦值;
(Ⅲ)求点C到平面B1DP的距离
(II)求二面角A-A1D-B的平面角的余弦值;
(Ⅲ)求点C到平面B1DP的距离
解:(Ⅰ)连接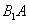 交
交 于
于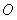
∵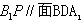 ,
,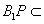 面
面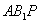 ,面
,面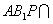 面
面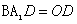
∴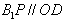
又O为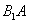 的中点,
的中点,
∴D为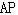 中点
中点
∴C1为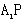 中点
中点
∴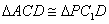
∴ ;
;
(Ⅱ)由题意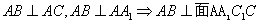 ,过B作
,过B作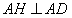 ,连接
,连接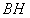 ,则
,则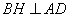
∴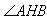 为
为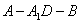 二面角的平面角
二面角的平面角
在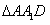 中,
中,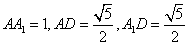
则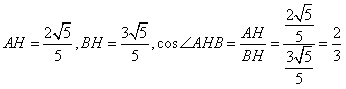 ;
;
(Ⅲ)因为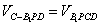
所以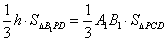 ,
,
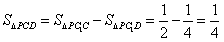
在 中,
中,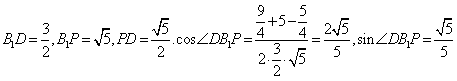
∴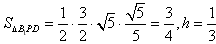 。
。
 交
交 于
于
∵
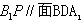 ,
,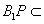 面
面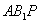 ,面
,面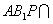 面
面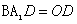
∴
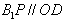
又O为
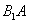 的中点,
的中点,∴D为
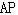 中点
中点∴C1为
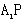 中点
中点∴
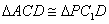
∴
 ;
;(Ⅱ)由题意
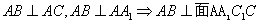 ,过B作
,过B作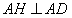 ,连接
,连接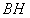 ,则
,则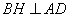
∴
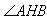 为
为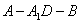 二面角的平面角
二面角的平面角在
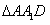 中,
中,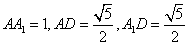
则
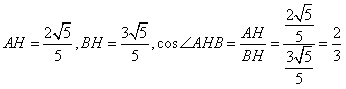 ;
;(Ⅲ)因为
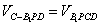
所以
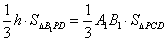 ,
,
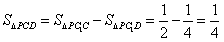
在
 中,
中,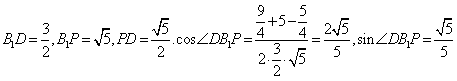
∴
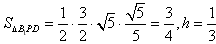 。
。
练习册系列答案
相关题目



