题目内容
设 且
且
(I)当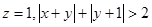 时,求
时,求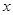 的取值范围;
的取值范围;
(II)当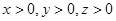 时,求
时,求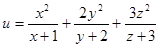 的最小值.
的最小值.
【答案】
(I)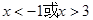 ;(II)
;(II)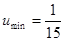
【解析】(I)当z=1时,可得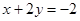 ,解出y代入
,解出y代入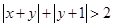 可得到关于x的绝对值不等式,再采用零点分段法,去绝对值,分段求解即可.
可得到关于x的绝对值不等式,再采用零点分段法,去绝对值,分段求解即可.
(II)根据柯西不等式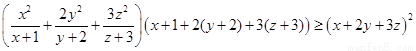 ,
,
然后转化为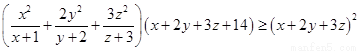 ,即可求出
,即可求出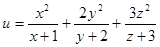 的最小值.
的最小值.
(I)当 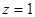 时,则
时,则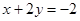 ,即
,即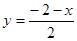 ,代入原不等式化简得
,代入原不等式化简得
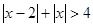 ,解得
,解得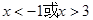
(II)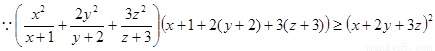
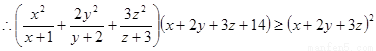
即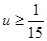 ,当且仅当
,当且仅当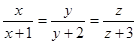 ,又
,又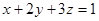 ,即
,即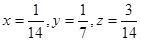 时,
时,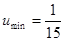

练习册系列答案
相关题目
 时,求函数f(x)的极值;
时,求函数f(x)的极值; 且
且 .
. 时,求实数
时,求实数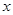 的取值范围;
的取值范围;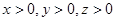 时,求
时,求 的最小值.
的最小值. 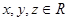 且
且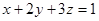 .
.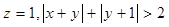 时,求实数
时,求实数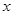 的取值范围;
的取值范围; 时,求
时,求 的最小值.
的最小值.