题目内容
设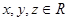 且
且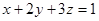 .
.
(I)当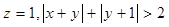 时,求实数
时,求实数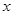 的取值范围;
的取值范围;
(II)当 时,求
时,求 的最小值.
的最小值.
【答案】
(I)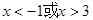 ;(II)
;(II)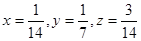 时,
时,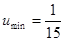 。
。
【解析】本试题主要是考查了不等式的证明,以及最值求解综合运用,属于中当试题。
(1)当 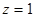 时,则
时,则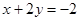 ,即
,即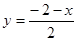 ,代入原不等式化简得
,代入原不等式化简得
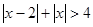 ,解得结论。
,解得结论。
(2)当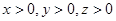 时,求
时,求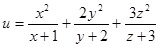 的最值问题可知转化为
的最值问题可知转化为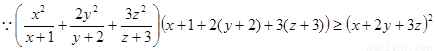 来证明即可。
来证明即可。
解:(I)当 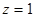 时,则
时,则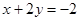 ,即
,即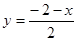 ,代入原不等式化简得
,代入原不等式化简得
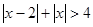 ,解得
,解得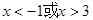 ………………5分
………………5分
(II)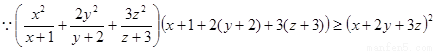
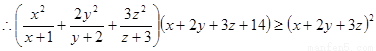
即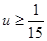 ,当且仅当
,当且仅当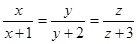 ,又
,又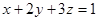 ,
,
即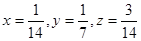 时,
时,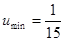 ………10分
………10分

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 且
且 .
. 时,求实数
时,求实数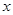 的取值范围;
的取值范围;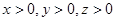 时,求
时,求 的最小值.
的最小值.  且
且
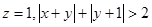 时,求
时,求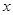 的取值范围;
的取值范围;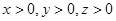 时,求
时,求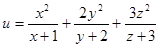 的最小值.
的最小值.  和
和 中,已知
中,已知 ,其中
,其中 且
且 。
。 ,求数列
,求数列 的前n项和;
的前n项和; 时,数列
时,数列 ,试问在区间[1,a]上是否存在实数b使得
,试问在区间[1,a]上是否存在实数b使得 ,若存在,求出b的一切可能的取值及相应的集合C;若不存在,说明理由。
,若存在,求出b的一切可能的取值及相应的集合C;若不存在,说明理由。