题目内容
在△ABC中,若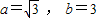 ,
, ,则c= .
,则c= .
【答案】分析:由已知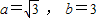 ,
,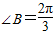 ,结合余弦定理可得,b2=a2+c2-2accosB,代入可得
,结合余弦定理可得,b2=a2+c2-2accosB,代入可得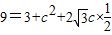 ,解方程可求.
,解方程可求.
解答:解:∵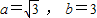 ,
,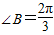 ,
,
由余弦定理可得,b2=a2+c2-2accosB
代入可得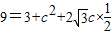
∴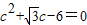 ∵c>0,∴
∵c>0,∴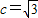
故答案为: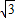
点评:本题主要考查了利用余弦定理解三角形,属于基础试题.
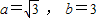 ,
,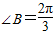 ,结合余弦定理可得,b2=a2+c2-2accosB,代入可得
,结合余弦定理可得,b2=a2+c2-2accosB,代入可得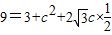 ,解方程可求.
,解方程可求.解答:解:∵
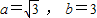 ,
,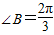 ,
,由余弦定理可得,b2=a2+c2-2accosB
代入可得
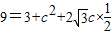
∴
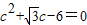 ∵c>0,∴
∵c>0,∴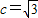
故答案为:
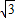
点评:本题主要考查了利用余弦定理解三角形,属于基础试题.

练习册系列答案
相关题目
在△ABC中,若acosA=bcosB,则△ABC的形状是( )
| A、等腰三角形 | B、直角三角形 | C、等腰直角三角形 | D、等腰或直角三角形 |
在△ABC中,若sinB=
,cosC=
,则cosA的值是( )
| 4 |
| 5 |
| 12 |
| 13 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|