题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 的交点为
的交点为![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设过定点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,连接
两点,连接![]() 并延长交抛物线的准线于点
并延长交抛物线的准线于点![]() ,当直线
,当直线![]() 恰与抛物线相切时,求直线
恰与抛物线相切时,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]()
【解析】
(Ⅰ))设![]() ,代入
,代入![]() ,得
,得![]() ,利用
,利用![]() 解得答案.
解得答案.
(Ⅱ)由题知直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() ,由
,由![]() 消去y整理得
消去y整理得![]() ,抛物线在点
,抛物线在点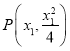 处的切线方程为
处的切线方程为![]() 利用韦达定理,整理得到答案.
利用韦达定理,整理得到答案.
(Ⅰ)设![]() ,代入
,代入![]() ,得
,得![]() ,
,
所以![]() ,
,![]() .
.
由题设得![]() ,解得
,解得![]() (舍去)或
(舍去)或![]() ,
,
∴C的方程为![]() .
.
(Ⅱ)由题知直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() ,
,
由![]() 消去y整理得
消去y整理得![]() ,
,
显然![]() .设
.设![]() ,
,![]() ,则
,则
抛物线在点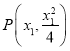 处的切线方程为
处的切线方程为![]() ,
,
令![]() ,得
,得![]() ,可得点
,可得点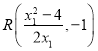 ,
,
由Q,F,R三点共线得![]() ,所以
,所以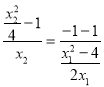 ,
,
即![]() ,整理得
,整理得![]() ,
,
所以![]() ,解得
,解得![]() ,即
,即![]() ,
,
故所求直线![]() 的方程为
的方程为![]() 或
或![]()

练习册系列答案
相关题目