��Ŀ����
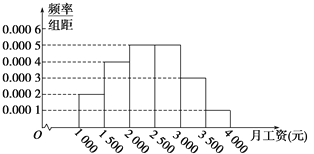
����Ŀ��ij���д�2014��ס����������̵�������������λ���䣩�������зֱ������ȡ100��������[ 0��10]����10��20]����20��30]����30��40]����40��50]���飬�õ�Ƶ�ʷֲ�ֱ��ͼ���£�
����ס����������̶������������������������
��1��д��Ƶ�ʷֲ�ֱ��ͼ���ף��е�![]() ��ֵ���Ǽ�����������������������������λ���䣩�ķ���ֱ�Ϊ
��ֵ���Ǽ�����������������������������λ���䣩�ķ���ֱ�Ϊ![]() ��
��![]() ���ԱȽ�
���ԱȽ�![]() ��
��![]() �Ĵ�С����ֻ��д�����ۣ�
�Ĵ�С����ֻ��д�����ۣ�
��2��������δ����ijһ����ס����������̵�������ǡ��һ������20������һ��������20��ĸ��ʣ�
��3����![]() ��ʾ��δ��3���ڼ������̵���������������20���������������������������Ƶ����Ϊ���ʣ���
��ʾ��δ��3���ڼ������̵���������������20���������������������������Ƶ����Ϊ���ʣ���![]() ����ѧ������
����ѧ������
���𰸡���1��![]() ��
��![]() ����2��0��42����3��0��9��
����2��0��42����3��0��9��
��������
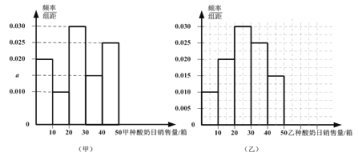
���⣨�����ɸ���С���ε������Ϊ1�������![]() ����Ƶ�ʷֲ�ֱ��ͼ�ɿ��������������ȽϷ�ɢ�����ҽ�Ϊ���У��ɴ˿ɵó�
����Ƶ�ʷֲ�ֱ��ͼ�ɿ��������������ȽϷ�ɢ�����ҽ�Ϊ���У��ɴ˿ɵó�![]() ��
��![]() �Ĵ�С��ϵ���������������¼�
�Ĵ�С��ϵ���������������¼�![]() ����δ����ijһ����������̵�������������20�䣻�¼�
����δ����ijһ����������̵�������������20�䣻�¼�![]() ����δ����ijһ����������̵�������������20�䣻�¼�
����δ����ijһ����������̵�������������20�䣻�¼�![]() ����δ����ijһ����ס����������̵�������ǡ��һ������20������һ��������20�䣻Ȼ��ֱ�����¼�
����δ����ijһ����ס����������̵�������ǡ��һ������20������һ��������20�䣻Ȼ��ֱ�����¼�![]() ���¼�
���¼�![]() �ĸ��ʣ������������¼��ĸ��ʳ˷����㹫ʽ���ɵó�����Ľ���������������������֪
�ĸ��ʣ������������¼��ĸ��ʳ˷����㹫ʽ���ɵó�����Ľ���������������������֪![]() �Ŀ���ȡֵΪ0��1��2��3��Ȼ������������ظ�����ĸ��ʼ��㹫ʽ�ֱ������Ӧ�ĸ��ʣ����ó���ֲ��м��ɣ�
�Ŀ���ȡֵΪ0��1��2��3��Ȼ������������ظ�����ĸ��ʼ��㹫ʽ�ֱ������Ӧ�ĸ��ʣ����ó���ֲ��м��ɣ�
����������������ɸ�С���ε������Ϊ1�ɵã�![]() ����֮��
����֮��
![]() ����Ƶ�ʷֲ�ֱ��ͼ�ɿ��������������ȽϷ�ɢ�����ҽ�Ϊ���У���Ҫ������
����Ƶ�ʷֲ�ֱ��ͼ�ɿ��������������ȽϷ�ɢ�����ҽ�Ϊ���У���Ҫ������![]() �䣬��
�䣬��
![]() ��
��
���������¼�![]() ����δ����ijһ����������̵�������������20�䣻�¼�
����δ����ijһ����������̵�������������20�䣻�¼�![]() ����δ����ijһ����������̵�������������20�䣻�¼�
����δ����ijһ����������̵�������������20�䣻�¼�![]() ����δ����ijһ����ס����������̵�������ǡ��һ������20������һ��������20�䣮��
����δ����ijһ����ס����������̵�������ǡ��һ������20������һ��������20�䣮��![]() ��
��![]() ������
������![]() ��
��
�������������֪��![]() �Ŀ���ȡֵΪ0��1��2��3��
�Ŀ���ȡֵΪ0��1��2��3��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
| 0��343 | 0��441 | 0��189 | 0��027 |
����![]() ����ѧ����
����ѧ����![]() ��
��

 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д� ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�