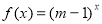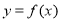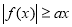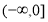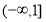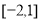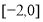题目内容
座落于我市红梅公园边的天宁宝塔堪称中华之最,也堪称佛塔世界之最.如图,已知天宁宝塔AB高度为150米,某大楼CD高度为90米,从大楼CD顶部C看天宁宝塔AB的张角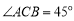 ,求天宁宝塔AB与大楼CD底部之间的距离BD.
,求天宁宝塔AB与大楼CD底部之间的距离BD.
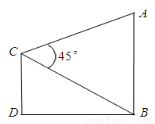
180米.
【解析】
试题分析:本题难点在于选择函数解析式模型,是用余弦定理解三角形,还是取直角三角形表示边.如用余弦定理解三角形,则得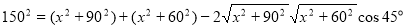 ,解此方程成为难点;如构造直角三角形就会减少运算量,即作CE
,解此方程成为难点;如构造直角三角形就会减少运算量,即作CE AB于E,构造直角三角形CBE和直角三角形CAE,利用两角和的正切公式得到关于BD的方程
AB于E,构造直角三角形CBE和直角三角形CAE,利用两角和的正切公式得到关于BD的方程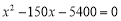 ,解此方程的运算量要少得多.将一个已知角分为两个角的和,这种思维不常见,须多加注意,深刻体会.
,解此方程的运算量要少得多.将一个已知角分为两个角的和,这种思维不常见,须多加注意,深刻体会.
试题解析:【解析】
如图作CE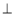 AB于E.因为AB∥CD,AB=150,CD=90,
AB于E.因为AB∥CD,AB=150,CD=90,
所以BE=90,AE=60.设CE=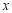 ,
,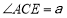 ,则
,则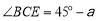 . 2分
. 2分
在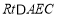 和
和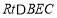 中,
中,
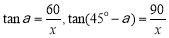 , 4分
, 4分
因为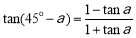 ,所以
,所以 . 8分
. 8分
化简得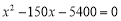 ,解得
,解得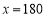 或
或 (舍去). 10分
(舍去). 10分
答:天宁宝塔AB与大楼CD底部之间的距离为180米. 12分
考点:两角和的正切公式,函数与方程.

练习册系列答案
相关题目