题目内容
甲、乙两人在罚球线互不影响地投球,命中的概率分别为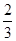 与
与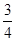 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.
(1)甲、乙两人在罚球线各投球一次,求两人得分之和 的数学期望;
的数学期望;
(2)甲、乙两人在罚球线各投球二次,求甲恰好比乙多得分的概率.
(1)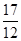
(2)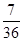
解析试题分析:解:(1)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事件B,则 与
与 相互独立,且P(A)=
相互独立,且P(A)=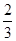 ,P(B)=
,P(B)=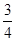 ,P(
,P(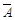 )=
)=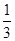 ,P(
,P(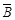 )=
)=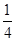 . 1分
. 1分
甲、乙两人得分之和 的可能取值为0、1、2, 2分
的可能取值为0、1、2, 2分
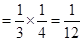
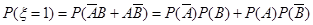
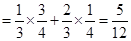
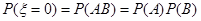
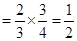 4分
4分
则 概率分布为:
概率分布为:
5分
0 1 2 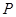
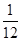
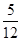
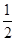
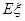 =0×
=0×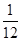 +1×
+1×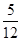 +2×
+2×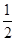 =
=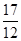 . 6分
. 6分
答:每人在罚球线各投球一次,两人得分之和 的数学期望为
的数学期望为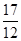 . 7分
. 7分
(2)设甲恰好比乙多得分为事件 ,甲得分且乙得
,甲得分且乙得 分为事件
分为事件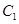 ,甲得
,甲得 分且乙得分为事件
分且乙得分为事件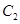 ,则
,则 =
=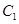 +
+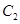 ,且
,且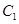 与
与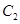 为互斥事件. 8分
为互斥事件. 8分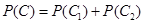
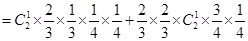
 11分
11分
答:甲、乙两人在罚球线各投球二次,甲恰好比乙多得分的概率为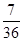 。 12分
。 12分
考点:分布列和独立事件的概率
点评:主要是通过实际问题来考查同学们运用概率公式来求解事件发生的概率以及分布列的运用,属于中档题。

练习册系列答案
相关题目
 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求 满足
满足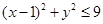 的概率.
的概率. ,求
,求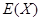 .
. 。
。 ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。
,每命中一次得2分,没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。
 件,其中有
件,其中有 件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品. ,求随机变量
,求随机变量