题目内容
选做题:(从所给的A,B两题中任选一题作答,若做两题,则按第一题A给分,共5分)A.在极坐标系(ρ,θ)(0≤θ≤2π)中,曲线ρ=2sinθ与ρcosθ=-1的交点坐标为 .
B.已知x,y,z∈R,有下列不等式:
(1)x2+y2+z2+3≥2(x+y+z);(2)
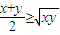 ;
;(3)|x+y|≤|x-2|+|y+2|;(4)x2+y2+z2≥xy+yz+zx.
其中一定成立的不等式的序号是 .
【答案】分析:A 把极坐标方程化为直角坐标方程求出交点的坐标,再把交点的坐标化为极坐标.
B 利用作差法及绝对值不等式的性质判断两个式子的大小关系.
解答:解:A 曲线ρ=2sinθ 即 ρ2=2ρsinθ,化为直角坐标方程为 x2+(y-1)2=1.
ρcosθ=-1即x=-1,把x=-1代入x2+(y-1)2=1可得交点坐标为(-1,1),
该点到原点的距离为 ,该点在第二象限的平分线上,
,该点在第二象限的平分线上,
故极角为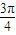 ,故交点的极坐标为
,故交点的极坐标为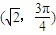 ,
,
故答案为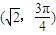 .
.
B∵x2+y2+z2+3-2(x+y+z)=(x-1)2+(y-1)2+(z-1)2≥0,∴x2+y2+z2+3≥2(x+y+z)成立.
故(1)正确.
当 x和y 为负数时,(2)显然不成立.
∵|x+y|=|x-2+y+2|≤|x-2|+|y+2|,故(3)正确.
∵x2+y2+z2-(xy+yz+zx )=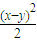 +
+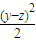 +
+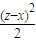 ≥0,故(4)正确.
≥0,故(4)正确.
点评:本题考查极坐标与直角坐标的互化,绝对值不等式的性质,变形是解题的关键.
B 利用作差法及绝对值不等式的性质判断两个式子的大小关系.
解答:解:A 曲线ρ=2sinθ 即 ρ2=2ρsinθ,化为直角坐标方程为 x2+(y-1)2=1.
ρcosθ=-1即x=-1,把x=-1代入x2+(y-1)2=1可得交点坐标为(-1,1),
该点到原点的距离为
 ,该点在第二象限的平分线上,
,该点在第二象限的平分线上,故极角为
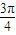 ,故交点的极坐标为
,故交点的极坐标为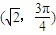 ,
,故答案为
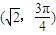 .
.B∵x2+y2+z2+3-2(x+y+z)=(x-1)2+(y-1)2+(z-1)2≥0,∴x2+y2+z2+3≥2(x+y+z)成立.
故(1)正确.
当 x和y 为负数时,(2)显然不成立.
∵|x+y|=|x-2+y+2|≤|x-2|+|y+2|,故(3)正确.
∵x2+y2+z2-(xy+yz+zx )=
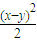 +
+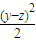 +
+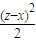 ≥0,故(4)正确.
≥0,故(4)正确.点评:本题考查极坐标与直角坐标的互化,绝对值不等式的性质,变形是解题的关键.

练习册系列答案
相关题目
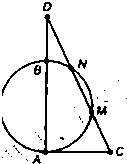 选做题(这里给出了3道选做题,考生只能从中选做一题,多答时按顺序只评第1位置题)
选做题(这里给出了3道选做题,考生只能从中选做一题,多答时按顺序只评第1位置题)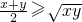 ;
;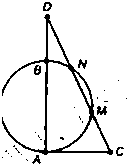 选做题(这里给出了3道选做题,考生只能从中选做一题,多答时按顺序只评第1位置题)
选做题(这里给出了3道选做题,考生只能从中选做一题,多答时按顺序只评第1位置题)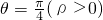 所表示的图形的交点的极坐标
所表示的图形的交点的极坐标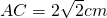 ,过C的割线CMN交AB的延长线于点D,CM=MN=ND,则AD的长等于________cm.
,过C的割线CMN交AB的延长线于点D,CM=MN=ND,则AD的长等于________cm.