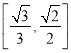题目内容
【题目】如图,四棱锥P﹣ABCD中,四边形ABCD是边长为2的正方形,△PAD为等边三角形,E,F分别为PC和BD的中点,且EF⊥CD.
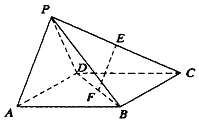
(1)证明:平面PAD⊥平面ABCD;
(2)求点C到平面PDB的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据中位线定理可证PA⊥CD,结合AD⊥CD可得CD⊥平面PAD,于是平面PAD⊥平面ABCD;
(2)计算△PBD的面积,根据VP﹣BCD=VC﹣PBD列方程计算点C到平面PDB的距离.
(1)因为E,F分别为PC和BD的中点,所以EF∥PA,
又因为EF⊥CD,所以PA⊥CD,
因为四边形ABCD是正方形,所以AD⊥CD,
又PA∩AD=A,PA平面PAD,AD平面PAD,所以CD⊥平面PAD,
又CD平面ABCD,所以平面PAD⊥平面ABCD.
(2)取AD的中点O,连接PO,
因为△PAD是等边三角形,AD=2,所以PO⊥AD,且PO![]() ,
,
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
所以PO⊥平面ABCD,
又四边形ABCD是边长为2的正方形,所以S△BCD![]() 2,
2,
所以VP﹣BCD![]() ,
,
连接OB,则OB![]() ,故PB
,故PB![]() 2
2![]() ,
,
又BD![]() 2
2![]() ,PD=2,
,PD=2,
所以S△PBD![]() ,
,
设C到平面PBD的距离为h,则VC﹣PBD![]() ,
,
整理得![]() ,解得h
,解得h![]() ,
,
即点C到平面PBD的距离为![]() .
.

【题目】某快餐连锁店,每天以200元的价格从总店购进早餐,然后以每份10元的价格出售.40份以内,总店收成本价每份5元,当天不能出售的早餐立即以1元的价格被总店回收,超过40份的未销售的部分总店成本价回收,然后进行环保处理.如果销售超过40份,则超过40份的利润需上缴总店.该快餐连锁店记录了100天早餐的销售量(单位:份),整理得下表:
日销售量 | 25 | 30 | 35 | 40 | 45 | 50 |
频数 | 10 | 16 | 28 | 24 | 14 | 8 |
完成下列问题:
(1)写出每天获得利润![]() 与销售早餐份数
与销售早餐份数![]() (
(![]() )的函数关系式;
)的函数关系式;
(2)估计每天利润不低于150元的概率;
(3)估计该快餐店每天的平均利润.