题目内容
设两圆C1、C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|=( )
| A.4 | B.4 | C.8 | D.8 |
C
解析试题分析:设圆的方程分别为 和
和 ,将点(4,1)代入可知
,将点(4,1)代入可知 和
和 ,两式分别解得
,两式分别解得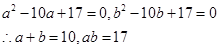
,那么两圆心的距离为|C1C2|=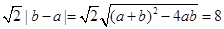 ,故选C
,故选C
考点:本试题考查了圆与圆的位置关系的运用。
点评:设出圆的方程,利用过公共点(4,1),且都与坐标轴相切说明了都在第一象限,求出圆心的坐标即可得到结论。属于中档题。

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
若函数 的图象在
的图象在 处的切线
处的切线 与圆
与圆 相离,则点
相离,则点 与圆C的位置关系是 ( )
与圆C的位置关系是 ( )
| A.点在圆外 | B.点在圆内 | C.点在圆上 | D.不能确定 |
若直线 过圆
过圆 的圆心,则
的圆心,则 的值为( )
的值为( )
A. | B. | C. | D. |
过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的方程是( )
| A.(x-3)2+(y+1)2=4 | B.(x-1)2+(y-1)2=4 |
| C.(x+3)2+(y-1)2=4 | D.(x+1)2+(y+1)2=4 |
若点P(3,-1)为圆 的弦AB的中点,则直线AB的方程为( )
的弦AB的中点,则直线AB的方程为( )
| A.x+y-2=0 | B.2x-y-7=0 | C.2x+y-5=0 | D.x-y-4=0 |
圆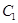 :
:  与圆
与圆 :
:  的位置关系是
的位置关系是
| A.外离 | B.相交 | C.内切 | D.外切 |
圆 关于
关于 对称的圆的方程是( )
对称的圆的方程是( )
A. | B. |
C. | D. |
过原点且倾斜角为 的直线被圆学
的直线被圆学 所截得的弦长为
所截得的弦长为
A. | B.2 | C. | D.2 |
 ,则直线倾斜角的取值范围是( )
,则直线倾斜角的取值范围是( )


